Question Number 165314 by mathlove last updated on 29/Jan/22
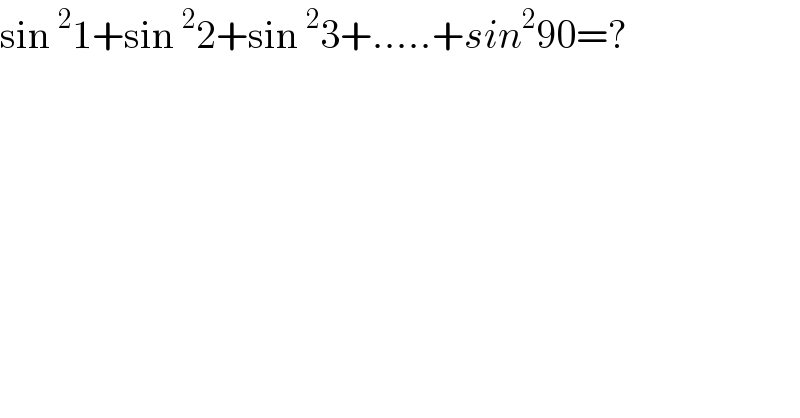
$$\mathrm{sin}\:^{\mathrm{2}} \mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{3}+…..+{sin}^{\mathrm{2}} \mathrm{90}=? \\ $$
Commented by cortano1 last updated on 29/Jan/22

$$\mathrm{45}.\mathrm{5}\: \\ $$
Commented by shunmisaki007 last updated on 29/Jan/22
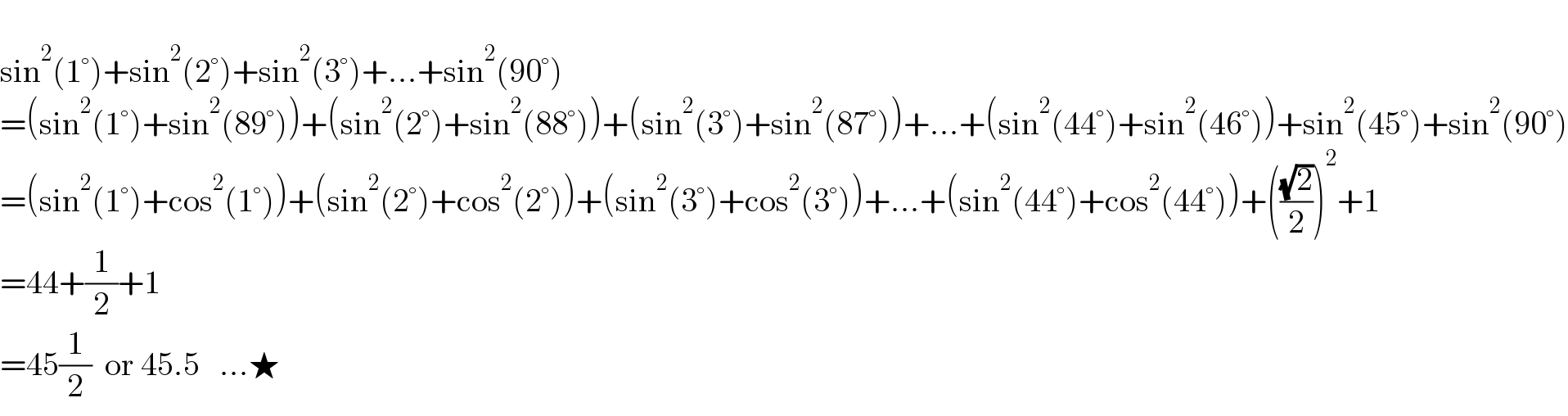
$$ \\ $$$$\mathrm{sin}^{\mathrm{2}} \left(\mathrm{1}°\right)+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}°\right)+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{3}°\right)+…+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{90}°\right) \\ $$$$=\left(\mathrm{sin}^{\mathrm{2}} \left(\mathrm{1}°\right)+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{89}°\right)\right)+\left(\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}°\right)+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{88}°\right)\right)+\left(\mathrm{sin}^{\mathrm{2}} \left(\mathrm{3}°\right)+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{87}°\right)\right)+…+\left(\mathrm{sin}^{\mathrm{2}} \left(\mathrm{44}°\right)+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{46}°\right)\right)+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{45}°\right)+\mathrm{sin}^{\mathrm{2}} \left(\mathrm{90}°\right) \\ $$$$=\left(\mathrm{sin}^{\mathrm{2}} \left(\mathrm{1}°\right)+\mathrm{cos}^{\mathrm{2}} \left(\mathrm{1}°\right)\right)+\left(\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}°\right)+\mathrm{cos}^{\mathrm{2}} \left(\mathrm{2}°\right)\right)+\left(\mathrm{sin}^{\mathrm{2}} \left(\mathrm{3}°\right)+\mathrm{cos}^{\mathrm{2}} \left(\mathrm{3}°\right)\right)+…+\left(\mathrm{sin}^{\mathrm{2}} \left(\mathrm{44}°\right)+\mathrm{cos}^{\mathrm{2}} \left(\mathrm{44}°\right)\right)+\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{1} \\ $$$$=\mathrm{44}+\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1} \\ $$$$=\mathrm{45}\frac{\mathrm{1}}{\mathrm{2}}\:\:\mathrm{or}\:\mathrm{45}.\mathrm{5}\:\:\:…\bigstar \\ $$
