Question Number 115169 by bobhans last updated on 24/Sep/20
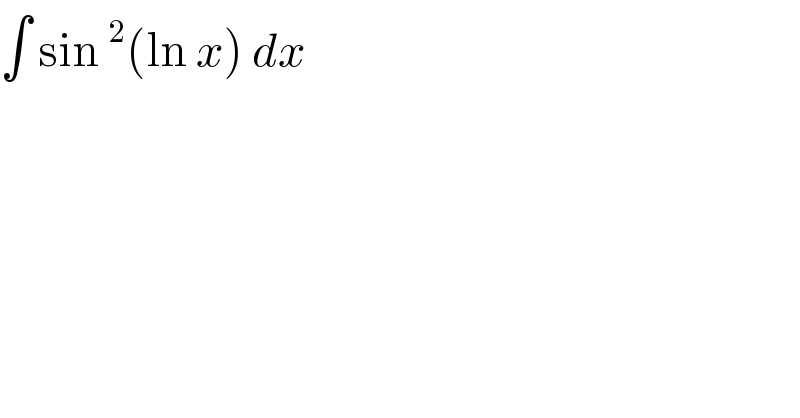
$$\int\:\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{ln}\:{x}\right)\:{dx}\: \\ $$
Answered by bobhans last updated on 24/Sep/20

Answered by Bird last updated on 24/Sep/20
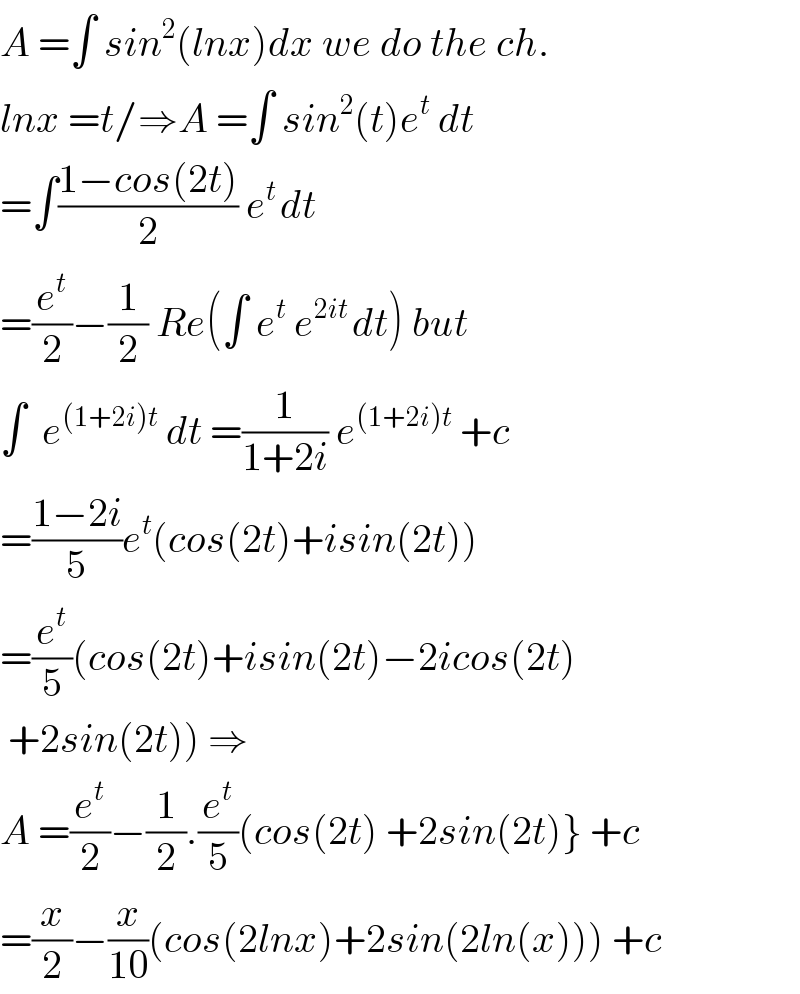
$${A}\:=\int\:{sin}^{\mathrm{2}} \left({lnx}\right){dx}\:{we}\:{do}\:{the}\:{ch}. \\ $$$${lnx}\:={t}/\Rightarrow{A}\:=\int\:{sin}^{\mathrm{2}} \left({t}\right){e}^{{t}} \:{dt} \\ $$$$=\int\frac{\mathrm{1}−{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\:{e}^{{t}\:} {dt} \\ $$$$=\frac{{e}^{{t}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\:{Re}\left(\int\:{e}^{{t}} \:{e}^{\mathrm{2}{it}\:} {dt}\right)\:{but} \\ $$$$\int\:\:{e}^{\left(\mathrm{1}+\mathrm{2}{i}\right){t}} \:{dt}\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}{i}}\:{e}^{\left(\mathrm{1}+\mathrm{2}{i}\right){t}} \:+{c} \\ $$$$=\frac{\mathrm{1}−\mathrm{2}{i}}{\mathrm{5}}{e}^{{t}} \left({cos}\left(\mathrm{2}{t}\right)+{isin}\left(\mathrm{2}{t}\right)\right) \\ $$$$=\frac{{e}^{{t}} }{\mathrm{5}}\left({cos}\left(\mathrm{2}{t}\right)+{isin}\left(\mathrm{2}{t}\right)−\mathrm{2}{icos}\left(\mathrm{2}{t}\right)\right. \\ $$$$\left.\:+\mathrm{2}{sin}\left(\mathrm{2}{t}\right)\right)\:\Rightarrow \\ $$$${A}\:=\frac{{e}^{{t}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}.\frac{{e}^{{t}} }{\mathrm{5}}\left({cos}\left(\mathrm{2}{t}\right)\:+\mathrm{2}{sin}\left(\mathrm{2}{t}\right)\right\}\:+{c} \\ $$$$=\frac{{x}}{\mathrm{2}}−\frac{{x}}{\mathrm{10}}\left({cos}\left(\mathrm{2}{lnx}\right)+\mathrm{2}{sin}\left(\mathrm{2}{ln}\left({x}\right)\right)\right)\:+{c} \\ $$
Answered by MJS_new last updated on 24/Sep/20
![without substitution sin^2 t =(((e^(it) −e^(−it) )/(2i)))^2 =−(((e^(2it) −1)^2 )/(4e^(2it) ))= [t=ln x] =−(((x^(2i) −1)^2 )/(4x^(2i) ))=(1/2)−(1/4)x^(2i) −(1/4)x^(−2i) ∫((1/2)−(1/4)x^(2i) −(1/4)x^(−2i) )dx= =(1/2)x−(1/(4(1+2i)))x^(1+2i) −(1/(4(1−2i)))x^(1−2i) = =(1/2)x−((1−2i)/(20))x^(1+2i) −((1+2i)/(20))x^(1−2i) = =(1/2)x−(1/(20))x(x^(2i) +x^(−2i) )+(i/(10))x(x^(2i) −x^(−2i) )= =(1/2)x−(1/(10))xcos (2ln x)−(1/5)xsin (2ln x)= =(x/5)(2+sin^2 (ln x)−2sin (ln x) cos (ln x))+C](https://www.tinkutara.com/question/Q115192.png)
$$\mathrm{without}\:\mathrm{substitution} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:{t}\:=\left(\frac{\mathrm{e}^{\mathrm{i}{t}} −\mathrm{e}^{−\mathrm{i}{t}} }{\mathrm{2i}}\right)^{\mathrm{2}} =−\frac{\left(\mathrm{e}^{\mathrm{2i}{t}} −\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4e}^{\mathrm{2i}{t}} }= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{ln}\:{x}\right] \\ $$$$=−\frac{\left({x}^{\mathrm{2i}} −\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}{x}^{\mathrm{2i}} }=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{2i}} −\frac{\mathrm{1}}{\mathrm{4}}{x}^{−\mathrm{2i}} \\ $$$$\int\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{2i}} −\frac{\mathrm{1}}{\mathrm{4}}{x}^{−\mathrm{2i}} \right){dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{x}−\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{1}+\mathrm{2i}\right)}{x}^{\mathrm{1}+\mathrm{2i}} −\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{1}−\mathrm{2i}\right)}{x}^{\mathrm{1}−\mathrm{2i}} = \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{x}−\frac{\mathrm{1}−\mathrm{2i}}{\mathrm{20}}{x}^{\mathrm{1}+\mathrm{2i}} −\frac{\mathrm{1}+\mathrm{2i}}{\mathrm{20}}{x}^{\mathrm{1}−\mathrm{2i}} = \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{x}−\frac{\mathrm{1}}{\mathrm{20}}{x}\left({x}^{\mathrm{2i}} +{x}^{−\mathrm{2i}} \right)+\frac{\mathrm{i}}{\mathrm{10}}{x}\left({x}^{\mathrm{2i}} −{x}^{−\mathrm{2i}} \right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{x}−\frac{\mathrm{1}}{\mathrm{10}}{x}\mathrm{cos}\:\left(\mathrm{2ln}\:{x}\right)−\frac{\mathrm{1}}{\mathrm{5}}{x}\mathrm{sin}\:\left(\mathrm{2ln}\:{x}\right)= \\ $$$$=\frac{{x}}{\mathrm{5}}\left(\mathrm{2}+\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{ln}\:{x}\right)−\mathrm{2sin}\:\left(\mathrm{ln}\:{x}\right)\:\mathrm{cos}\:\left(\mathrm{ln}\:{x}\right)\right)+{C} \\ $$
