Question Number 145979 by iloveisrael last updated on 09/Jul/21
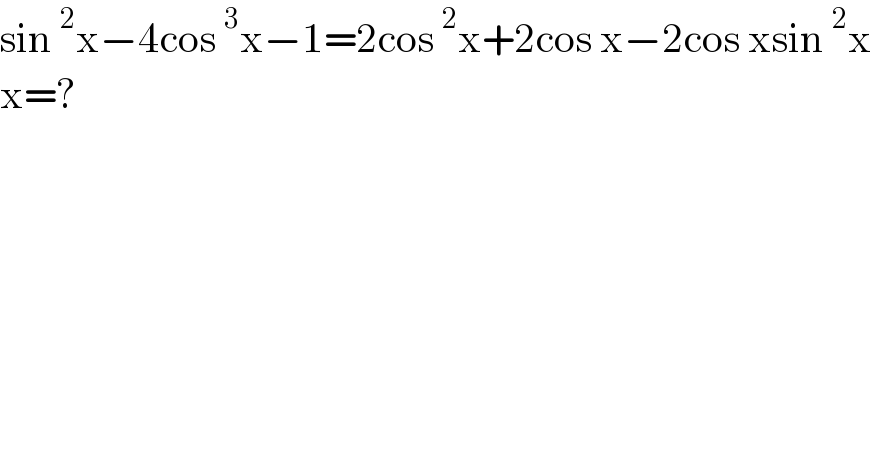
$$\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}−\mathrm{4cos}\:^{\mathrm{3}} \mathrm{x}−\mathrm{1}=\mathrm{2cos}\:^{\mathrm{2}} \mathrm{x}+\mathrm{2cos}\:\mathrm{x}−\mathrm{2cos}\:\mathrm{xsin}\:^{\mathrm{2}} \mathrm{x} \\ $$$$\mathrm{x}=? \\ $$
Answered by Olaf_Thorendsen last updated on 10/Jul/21
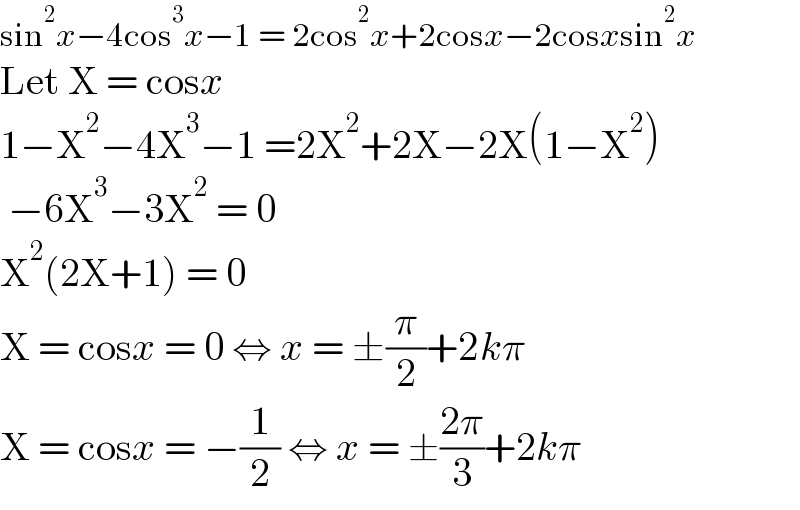
$$\mathrm{sin}^{\mathrm{2}} {x}−\mathrm{4cos}^{\mathrm{3}} {x}−\mathrm{1}\:=\:\mathrm{2cos}^{\mathrm{2}} {x}+\mathrm{2cos}{x}−\mathrm{2cos}{x}\mathrm{sin}^{\mathrm{2}} {x} \\ $$$$\mathrm{Let}\:\mathrm{X}\:=\:\mathrm{cos}{x} \\ $$$$\mathrm{1}−\mathrm{X}^{\mathrm{2}} −\mathrm{4X}^{\mathrm{3}} −\mathrm{1}\:=\mathrm{2X}^{\mathrm{2}} +\mathrm{2X}−\mathrm{2X}\left(\mathrm{1}−\mathrm{X}^{\mathrm{2}} \right) \\ $$$$\:−\mathrm{6X}^{\mathrm{3}} −\mathrm{3X}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\mathrm{X}^{\mathrm{2}} \left(\mathrm{2X}+\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$$\mathrm{X}\:=\:\mathrm{cos}{x}\:=\:\mathrm{0}\:\Leftrightarrow\:{x}\:=\:\pm\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi \\ $$$$\mathrm{X}\:=\:\mathrm{cos}{x}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\:\Leftrightarrow\:{x}\:=\:\pm\frac{\mathrm{2}\pi}{\mathrm{3}}+\mathrm{2}{k}\pi \\ $$
