Question Number 190993 by mathlove last updated on 16/Apr/23
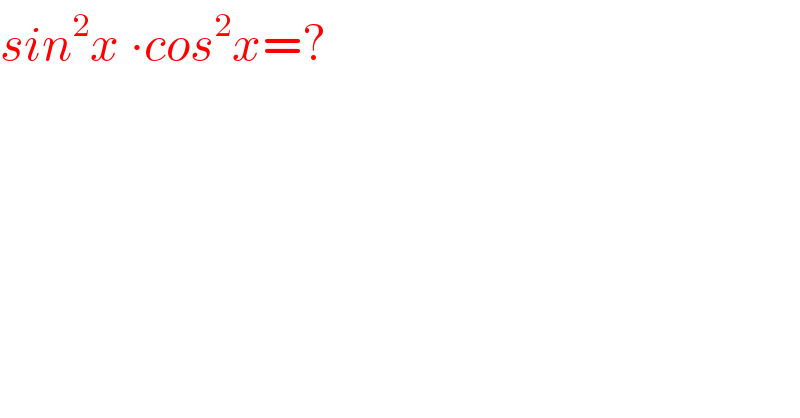
$${sin}^{\mathrm{2}} {x}\:\centerdot{cos}^{\mathrm{2}} {x}=? \\ $$
Answered by cortano12 last updated on 16/Apr/23

$$\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{2x} \\ $$
Answered by mustafazaheen last updated on 16/Apr/23
![=[(2/2)sin(x)∙cos(x)][(2/2)sin(x)∙cos(x)] =((sin(2x))/2)×((sin(2x))/2) =(1/4)sin^2 (2x)](https://www.tinkutara.com/question/Q190995.png)
$$=\left[\frac{\mathrm{2}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{x}\right)\centerdot\mathrm{cos}\left(\mathrm{x}\right)\right]\left[\frac{\mathrm{2}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{x}\right)\centerdot\mathrm{cos}\left(\mathrm{x}\right)\right] \\ $$$$=\frac{\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{2}}×\frac{\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2x}\right) \\ $$
Answered by manxsol last updated on 16/Apr/23
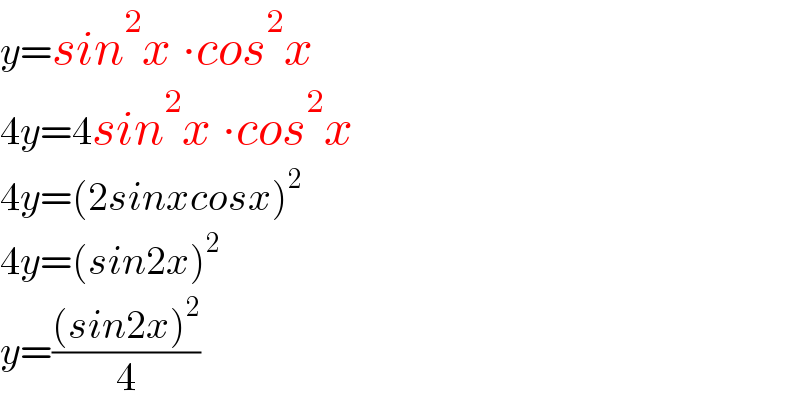
$${y}={sin}^{\mathrm{2}} {x}\:\centerdot{cos}^{\mathrm{2}} {x} \\ $$$$\mathrm{4}{y}=\mathrm{4}{sin}^{\mathrm{2}} {x}\:\centerdot{cos}^{\mathrm{2}} {x} \\ $$$$\mathrm{4}{y}=\left(\mathrm{2}{sinxcosx}\right)^{\mathrm{2}} \\ $$$$\mathrm{4}{y}=\left({sin}\mathrm{2}{x}\right)^{\mathrm{2}} \\ $$$${y}=\frac{\left({sin}\mathrm{2}{x}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$
