Menu Close

sin-2-x-dx-1-sin-x-cos-x-

Tinku Tara 0 Comments
Pin




Question Number 106709 by bemath last updated on 06/Aug/20
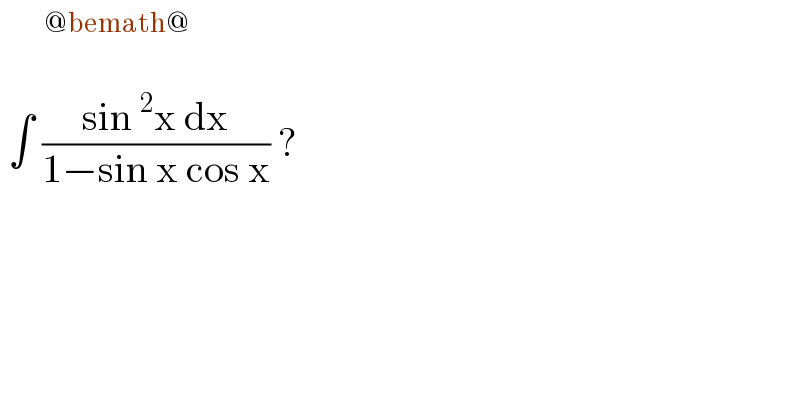
∫ ((sin^2 x dx)/(1−sin x cos x)) ?
$$ \\ $$$$\:\int\:\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}}{\mathrm{1}−\mathrm{sin}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{x}}\:? \\ $$
Answered by john santu last updated on 06/Aug/20
^(@JS@) I=∫ (((1/2)−(1/2)cos 2x)/(1−((sin 2x)/2))) dx = ∫ ((1−cos 2x)/(2−sin 2x)) dx I=∫ (dx/(2−sin 2x)) −∫ ((cos 2x)/(2−sin 2x)) dx set I_1 =∫ (dx/(2−sin 2x)) [ let tan x = ♭ ] I_1 = ∫ ((((1/(♭^2 +1))) d♭)/(2−(((2♭)/(♭^2 +1))))) = ∫ (d♭/(2♭^2 −2♭+2)) I_1 =(1/2)∫ (d♭/((♭−(1/2))^2 +(((√3)/2))^2 )) I_2 =∫ ((cos 2x dx)/(2−sin 2x)) = −(1/2)∫ ((d(2−sin 2x))/(2−sin 2x)) I_1 =−(1/2)ln ∣2−sin 2x∣ ∴ I = I_1 −I_2
$$\:\:\:\:\overset{@\mathrm{JS}@} {\:} \\ $$$$\mathrm{I}=\int\:\frac{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2x}}{\mathrm{1}−\frac{\mathrm{sin}\:\mathrm{2x}}{\mathrm{2}}}\:\mathrm{dx}\:=\:\int\:\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2x}}{\mathrm{2}−\mathrm{sin}\:\mathrm{2x}}\:\mathrm{dx} \\ $$$$\mathrm{I}=\int\:\frac{\mathrm{dx}}{\mathrm{2}−\mathrm{sin}\:\mathrm{2x}}\:−\int\:\frac{\mathrm{cos}\:\mathrm{2x}}{\mathrm{2}−\mathrm{sin}\:\mathrm{2x}}\:\mathrm{dx}\: \\ $$$$\mathrm{set}\:\mathrm{I}_{\mathrm{1}} =\int\:\frac{\mathrm{dx}}{\mathrm{2}−\mathrm{sin}\:\mathrm{2x}}\:\left[\:\mathrm{let}\:\mathrm{tan}\:\mathrm{x}\:=\:\flat\:\right] \\ $$$$\mathrm{I}_{\mathrm{1}} =\:\int\:\frac{\left(\frac{\mathrm{1}}{\flat^{\mathrm{2}} +\mathrm{1}}\right)\:\mathrm{d}\flat}{\mathrm{2}−\left(\frac{\mathrm{2}\flat}{\flat^{\mathrm{2}} +\mathrm{1}}\right)}\:=\:\int\:\frac{\mathrm{d}\flat}{\mathrm{2}\flat^{\mathrm{2}} −\mathrm{2}\flat+\mathrm{2}} \\ $$$$\mathrm{I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{d}\flat}{\left(\flat−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{I}_{\mathrm{2}} =\int\:\frac{\mathrm{cos}\:\mathrm{2x}\:\mathrm{dx}}{\mathrm{2}−\mathrm{sin}\:\mathrm{2x}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{d}\left(\mathrm{2}−\mathrm{sin}\:\mathrm{2x}\right)}{\mathrm{2}−\mathrm{sin}\:\mathrm{2x}} \\ $$$$\mathrm{I}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{2}−\mathrm{sin}\:\mathrm{2x}\mid\: \\ $$$$\therefore\:\mathrm{I}\:=\:\mathrm{I}_{\mathrm{1}} −\mathrm{I}_{\mathrm{2}} \: \\ $$
Answered by Dwaipayan Shikari last updated on 06/Aug/20
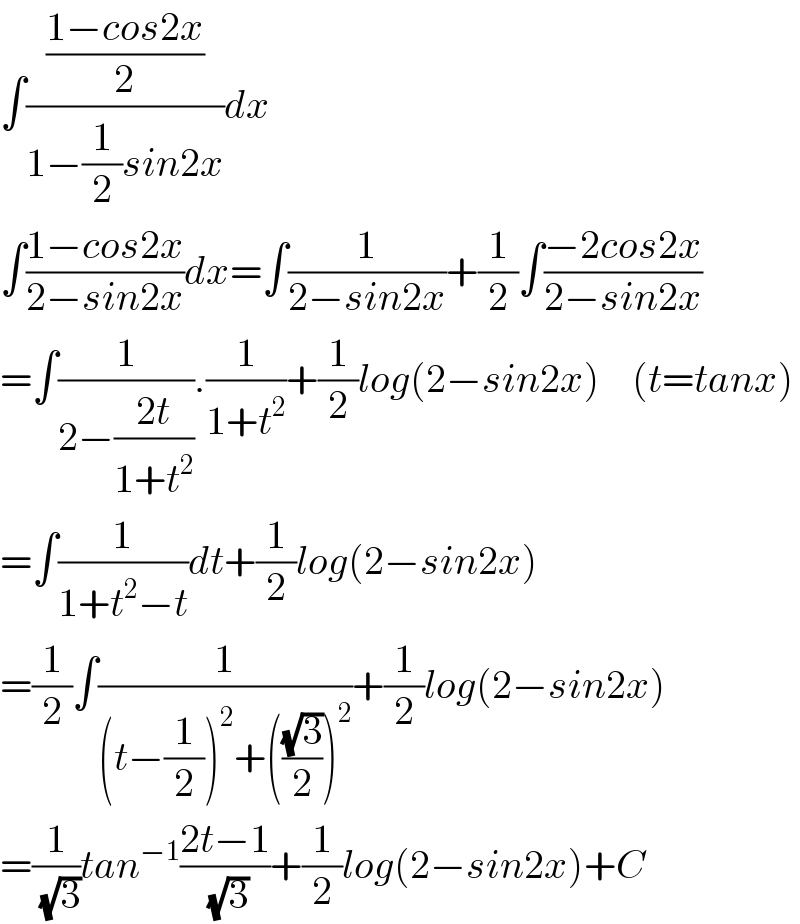
∫(((1−cos2x)/2)/(1−(1/2)sin2x))dx ∫((1−cos2x)/(2−sin2x))dx=∫(1/(2−sin2x))+(1/2)∫((−2cos2x)/(2−sin2x)) =∫(1/(2−((2t)/(1+t^2 )))).(1/(1+t^2 ))+(1/2)log(2−sin2x) (t=tanx) =∫(1/(1+t^2 −t))dt+(1/2)log(2−sin2x) =(1/2)∫(1/((t−(1/2))^2 +(((√3)/2))^2 ))+(1/2)log(2−sin2x) =(1/( (√3)))tan^(−1) ((2t−1)/( (√3)))+(1/2)log(2−sin2x)+C
$$\int\frac{\frac{\mathrm{1}−{cos}\mathrm{2}{x}}{\mathrm{2}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}{x}}{dx} \\ $$$$\int\frac{\mathrm{1}−{cos}\mathrm{2}{x}}{\mathrm{2}−{sin}\mathrm{2}{x}}{dx}=\int\frac{\mathrm{1}}{\mathrm{2}−{sin}\mathrm{2}{x}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{−\mathrm{2}{cos}\mathrm{2}{x}}{\mathrm{2}−{sin}\mathrm{2}{x}} \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{2}−\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}.\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{2}−{sin}\mathrm{2}{x}\right)\:\:\:\:\left({t}={tanx}\right) \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} −{t}}{dt}+\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{2}−{sin}\mathrm{2}{x}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{\left({t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{2}−{sin}\mathrm{2}{x}\right) \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \frac{\mathrm{2}{t}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}+\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{2}−{sin}\mathrm{2}{x}\right)+{C} \\ $$
Answered by mathmax by abdo last updated on 07/Aug/20
I =∫ ((sin^2 x)/(1−sinx cosx))dx ⇒ I =∫ ((1−cos(2x))/(2(1−(1/2)sin(2x))))dx =∫ ((1−cos(2x))/(2−sin(2x)))dx =_(tanx =t) ∫ ((1−((1−t^2 )/(1+t^2 )))/(2−((2t)/(1+t^2 ))))×(dt/(1+t^2 )) =∫ ((1+t^2 −1+t^2 )/(2+2t^2 −2t)) (dt/(1+t^2 )) =(1/2)∫ ((2t^2 )/((1+t^2 )(t^2 −t+1)))dt =∫ (t^2 /((t^2 +1)(t^2 −t +1)))dt =−∫ t((1/(t^2 +1))−(1/(t^2 −t +1)))dt =∫ ( (t/(t^2 −t+1))−(t/(t^2 +1)))dt =(1/2)∫ ((2t−1−1)/(t^2 −t+1))dt−(1/2)∫ ((2t)/(t^2 +1))dt =(1/2)ln(t^2 −t +1)−(1/2)ln(t^2 +1)−(1/2) ∫ (dt/(t^2 −t +1)) we have ∫ (dt/(t^2 −t +1)) =∫ (dt/((t−(1/2))^2 +(3/4))) =_(t−(1/2)=((√3)/2)u) (4/3) ∫ (1/(1+u^2 )).((√3)/2)du =(2/( (√3)))arctan(u)+c =(2/( (√3)))arctan(((2t−1)/( (√3)))) ⇒ I =(1/2)ln(t^2 −t+1)−(1/2)ln(t^2 +1)−(1/( (√3))) arctan(((2t−1)/( (√3)))) +C I=(1/2)ln(((tan^2 x−tanx +1)/(tan^2 x +1)))−(1/( (√3)))arctan(((2tanx −1)/( (√3)))) +C
$$\mathrm{I}\:=\int\:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{1}−\mathrm{sinx}\:\mathrm{cosx}}\mathrm{dx}\:\Rightarrow\:\mathrm{I}\:=\int\:\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2x}\right)\right)}\mathrm{dx} \\ $$$$=\int\:\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}−\mathrm{sin}\left(\mathrm{2x}\right)}\mathrm{dx}\:\:=_{\mathrm{tanx}\:=\mathrm{t}} \:\:\int\:\frac{\mathrm{1}−\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}{\mathrm{2}−\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}×\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$=\int\:\frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} −\mathrm{1}+\mathrm{t}^{\mathrm{2}} }{\mathrm{2}+\mathrm{2t}^{\mathrm{2}} −\mathrm{2t}}\:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{2t}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}\right)}\mathrm{dt} \\ $$$$=\int\:\:\frac{\mathrm{t}^{\mathrm{2}} }{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} −\mathrm{t}\:+\mathrm{1}\right)}\mathrm{dt}\:=−\int\:\mathrm{t}\left(\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\mathrm{t}\:+\mathrm{1}}\right)\mathrm{dt} \\ $$$$=\int\:\left(\:\frac{\mathrm{t}}{\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}}−\frac{\mathrm{t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\right)\mathrm{dt}\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{2t}−\mathrm{1}−\mathrm{1}}{\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}}\mathrm{dt}−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{2t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{t}\:+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{t}\:+\mathrm{1}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\int\:\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\mathrm{t}\:+\mathrm{1}}\:=\int\:\frac{\mathrm{dt}}{\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}\:=_{\mathrm{t}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{u}} \frac{\mathrm{4}}{\mathrm{3}}\:\:\int\:\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }.\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{du} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\mathrm{u}\right)+\mathrm{c}\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{\mathrm{2t}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\mathrm{arctan}\left(\frac{\mathrm{2t}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:+\mathrm{C} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{tan}^{\mathrm{2}} \mathrm{x}−\mathrm{tanx}\:+\mathrm{1}}{\mathrm{tan}^{\mathrm{2}} \mathrm{x}\:+\mathrm{1}}\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{arctan}\left(\frac{\mathrm{2tanx}\:−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:+\mathrm{C} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *