Menu Close

sin-2-x-sec-2-x-2-1-x-2-tan-x-sin-1-x-1-x-2-1-tan-2-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 130544 by EDWIN88 last updated on 26/Jan/21
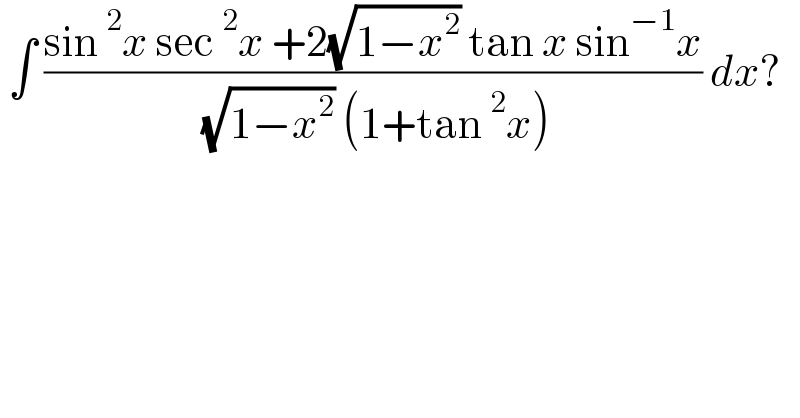
∫ ((sin^2 x sec^2 x +2(√(1−x^2 )) tan x sin^(−1) x)/( (√(1−x^2 )) (1+tan^2 x))) dx?
$$\:\int\:\frac{\mathrm{sin}\:^{\mathrm{2}} {x}\:\mathrm{sec}\:^{\mathrm{2}} {x}\:+\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\mathrm{tan}\:{x}\:\mathrm{sin}^{−\mathrm{1}} {x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {x}\right)}\:{dx}? \\ $$
Answered by mindispower last updated on 26/Jan/21
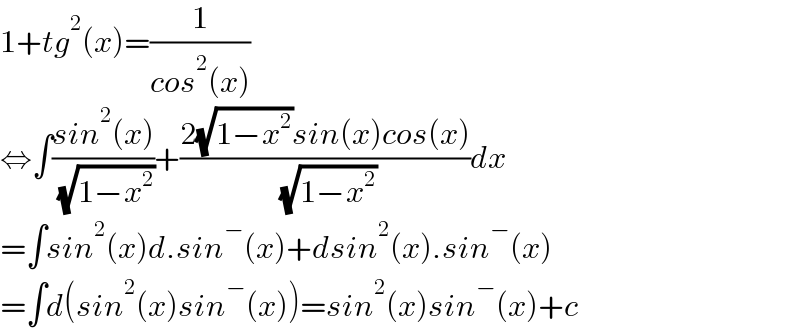
1+tg^2 (x)=(1/(cos^2 (x))) ⇔∫((sin^2 (x))/( (√(1−x^2 ))))+((2(√(1−x^2 ))sin(x)cos(x))/( (√(1−x^2 ))))dx =∫sin^2 (x)d.sin^− (x)+dsin^2 (x).sin^− (x) =∫d(sin^2 (x)sin^− (x))=sin^2 (x)sin^− (x)+c
$$\mathrm{1}+{tg}^{\mathrm{2}} \left({x}\right)=\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left({x}\right)} \\ $$$$\Leftrightarrow\int\frac{{sin}^{\mathrm{2}} \left({x}\right)}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}+\frac{\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{sin}\left({x}\right){cos}\left({x}\right)}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$$=\int{sin}^{\mathrm{2}} \left({x}\right){d}.{sin}^{−} \left({x}\right)+{dsin}^{\mathrm{2}} \left({x}\right).{sin}^{−} \left({x}\right) \\ $$$$=\int{d}\left({sin}^{\mathrm{2}} \left({x}\right){sin}^{−} \left({x}\right)\right)={sin}^{\mathrm{2}} \left({x}\right){sin}^{−} \left({x}\right)+{c} \\ $$
Answered by liberty last updated on 26/Jan/21
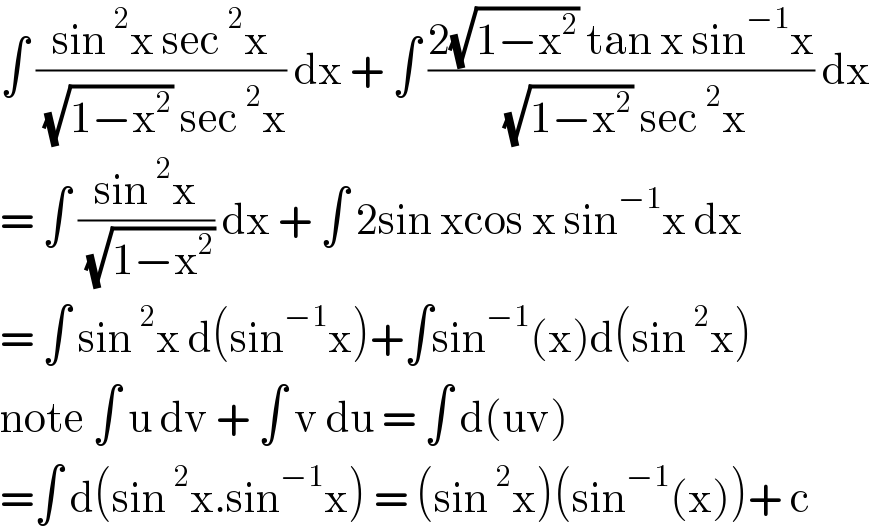
∫ ((sin^2 x sec^2 x)/( (√(1−x^2 )) sec^2 x)) dx + ∫ ((2(√(1−x^2 )) tan x sin^(−1) x)/( (√(1−x^2 )) sec^2 x)) dx = ∫ ((sin^2 x)/( (√(1−x^2 )))) dx + ∫ 2sin xcos x sin^(−1) x dx = ∫ sin^2 x d(sin^(−1) x)+∫sin^(−1) (x)d(sin^2 x) note ∫ u dv + ∫ v du = ∫ d(uv) =∫ d(sin^2 x.sin^(−1) x) = (sin^2 x)(sin^(−1) (x))+ c
$$\int\:\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}}\:\mathrm{dx}\:+\:\int\:\frac{\mathrm{2}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\mathrm{tan}\:\mathrm{x}\:\mathrm{sin}^{−\mathrm{1}} \mathrm{x}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}}\:\mathrm{dx}\: \\ $$$$=\:\int\:\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx}\:+\:\int\:\mathrm{2sin}\:\mathrm{xcos}\:\mathrm{x}\:\mathrm{sin}^{−\mathrm{1}} \mathrm{x}\:\mathrm{dx} \\ $$$$=\:\int\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{d}\left(\mathrm{sin}^{−\mathrm{1}} \mathrm{x}\right)+\int\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{x}\right)\mathrm{d}\left(\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right) \\ $$$$\mathrm{note}\:\int\:\mathrm{u}\:\mathrm{dv}\:+\:\int\:\mathrm{v}\:\mathrm{du}\:=\:\int\:\mathrm{d}\left(\mathrm{uv}\right) \\ $$$$=\int\:\mathrm{d}\left(\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}.\mathrm{sin}^{−\mathrm{1}} \mathrm{x}\right)\:=\:\left(\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{x}\right)\right)+\:\mathrm{c} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *