Question Number 163580 by mkam last updated on 08/Jan/22
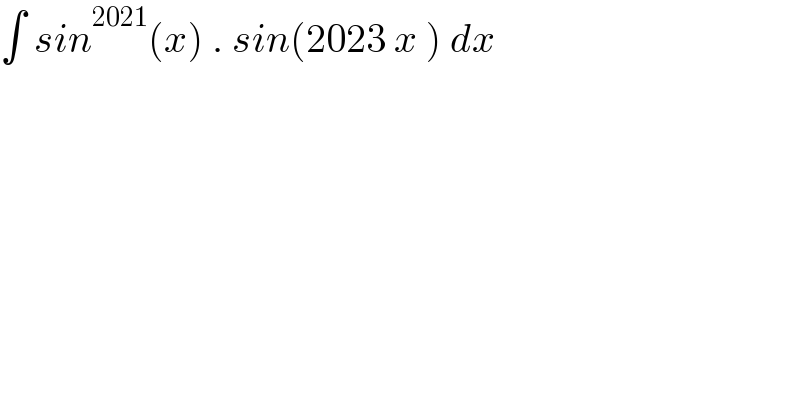
$$\int\:{sin}^{\mathrm{2021}} \left({x}\right)\:.\:{sin}\left(\mathrm{2023}\:{x}\:\right)\:{dx}\: \\ $$
Commented by mkam last updated on 08/Jan/22

$$?????? \\ $$
Answered by abdullahhhhh last updated on 08/Jan/22
![I=∫sin(2022x+x) sin^(2021) x dx ∫sin^(2021) x [sin(2022x)cosx(x)+cosx(2022x) sinx] I=∫[cosx sin^(2021) x sin(2022x)] dx+∫sin^(2022) x cos(2022x) dx I=I_1 (By parts)+I_2 I_1 =∫cosx sin^(2021) x sin(2022x) dx u=sin(2022x) dv =cosx sin^(2021) x du=2022 cos(2022x) v=((sin^(2022) x)/(2022)) (1/(2022)) sin(2022x) sin^(2022) x−∫cos(2022) sin^(2022) x dx I_1 =((sin(2022x) sin^(2022) x)/(2022))−I_2 I=((sin(2022x) sin^(2022) x)/(2022))+C](https://www.tinkutara.com/question/Q163626.png)
$$\boldsymbol{\mathrm{I}}=\int\boldsymbol{\mathrm{sin}}\left(\mathrm{2022}\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{x}}\right)\:\boldsymbol{\mathrm{sin}}^{\mathrm{2021}} \boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{dx}} \\ $$$$\int\boldsymbol{{sin}}^{\mathrm{2021}} \boldsymbol{{x}}\:\left[\boldsymbol{{sin}}\left(\mathrm{2022}\boldsymbol{{x}}\right)\boldsymbol{{cosx}}\left(\boldsymbol{{x}}\right)+\boldsymbol{{cosx}}\left(\mathrm{2022}\boldsymbol{{x}}\right)\:\boldsymbol{{sinx}}\right] \\ $$$$\boldsymbol{\mathrm{I}}=\int\left[\boldsymbol{\mathrm{cosx}}\:\boldsymbol{\mathrm{sin}}^{\mathrm{2021}} \boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{sin}}\left(\mathrm{2022}\boldsymbol{\mathrm{x}}\right)\right]\:\boldsymbol{\mathrm{dx}}+\int\boldsymbol{\mathrm{sin}}^{\mathrm{2022}} \boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{cos}}\left(\mathrm{2022}\boldsymbol{\mathrm{x}}\right)\:\boldsymbol{\mathrm{dx}} \\ $$$$\boldsymbol{\mathrm{I}}=\boldsymbol{\mathrm{I}}_{\mathrm{1}} \left(\boldsymbol{\mathrm{By}}\:\boldsymbol{\mathrm{parts}}\right)+\boldsymbol{{I}}_{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{I}}_{\mathrm{1}} =\int\boldsymbol{\mathrm{cosx}}\:\boldsymbol{\mathrm{sin}}^{\mathrm{2021}} \boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{sin}}\left(\mathrm{2022}\boldsymbol{\mathrm{x}}\right)\:\boldsymbol{\mathrm{dx}} \\ $$$$\boldsymbol{\mathrm{u}}=\boldsymbol{\mathrm{sin}}\left(\mathrm{2022}\boldsymbol{\mathrm{x}}\right)\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{dv}}\:=\boldsymbol{\mathrm{cosx}}\:\boldsymbol{\mathrm{sin}}^{\mathrm{2021}} \boldsymbol{\mathrm{x}} \\ $$$$\boldsymbol{\mathrm{du}}=\mathrm{2022}\:\boldsymbol{\mathrm{cos}}\left(\mathrm{2022}\boldsymbol{\mathrm{x}}\right)\:\:\:\:\boldsymbol{\mathrm{v}}=\frac{\boldsymbol{\mathrm{sin}}^{\mathrm{2022}} \boldsymbol{\mathrm{x}}}{\mathrm{2022}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2022}}\:\:\boldsymbol{\mathrm{sin}}\left(\mathrm{2022}\boldsymbol{\mathrm{x}}\right)\:\boldsymbol{\mathrm{sin}}^{\mathrm{2022}} \boldsymbol{\mathrm{x}}−\int\boldsymbol{\mathrm{cos}}\left(\mathrm{2022}\right)\:\boldsymbol{\mathrm{sin}}^{\mathrm{2022}} \boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{dx}} \\ $$$$\boldsymbol{\mathrm{I}}_{\mathrm{1}} =\frac{\boldsymbol{\mathrm{sin}}\left(\mathrm{2022}\boldsymbol{\mathrm{x}}\right)\:\boldsymbol{\mathrm{sin}}^{\mathrm{2022}} \boldsymbol{\mathrm{x}}}{\mathrm{2022}}−\boldsymbol{\mathrm{I}}_{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{I}}=\frac{\boldsymbol{\mathrm{sin}}\left(\mathrm{2022}\boldsymbol{\mathrm{x}}\right)\:\boldsymbol{\mathrm{sin}}^{\mathrm{2022}} \boldsymbol{\mathrm{x}}}{\mathrm{2022}}+\boldsymbol{\mathrm{C}} \\ $$
