Question Number 112481 by bemath last updated on 08/Sep/20
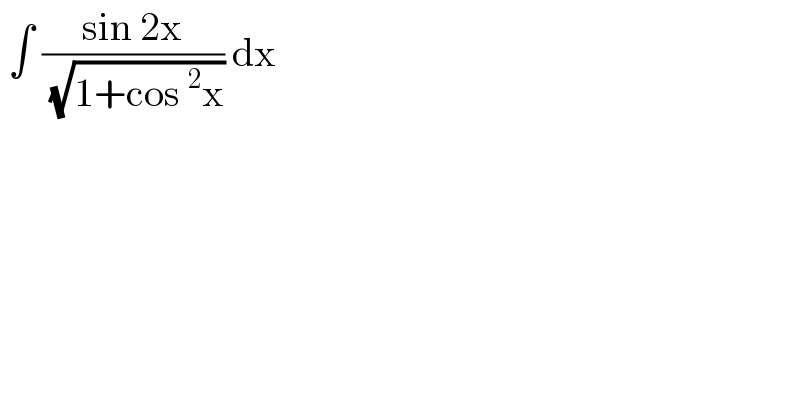
$$\:\int\:\frac{\mathrm{sin}\:\mathrm{2x}}{\:\sqrt{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}}\:\mathrm{dx}\: \\ $$
Answered by john santu last updated on 08/Sep/20
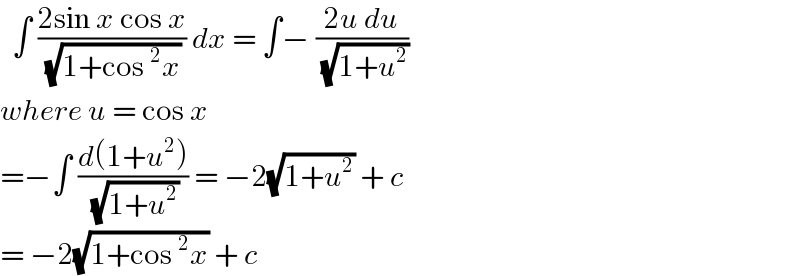
$$\:\:\int\:\frac{\mathrm{2sin}\:{x}\:\mathrm{cos}\:{x}}{\:\sqrt{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} {x}}}\:{dx}\:=\:\int−\:\frac{\mathrm{2}{u}\:{du}}{\:\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }} \\ $$$${where}\:{u}\:=\:\mathrm{cos}\:{x} \\ $$$$=−\int\:\frac{{d}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }}\:=\:−\mathrm{2}\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }\:+\:{c} \\ $$$$=\:−\mathrm{2}\sqrt{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} {x}}\:+\:{c}\: \\ $$
