Question Number 128073 by I want to learn more last updated on 04/Jan/21
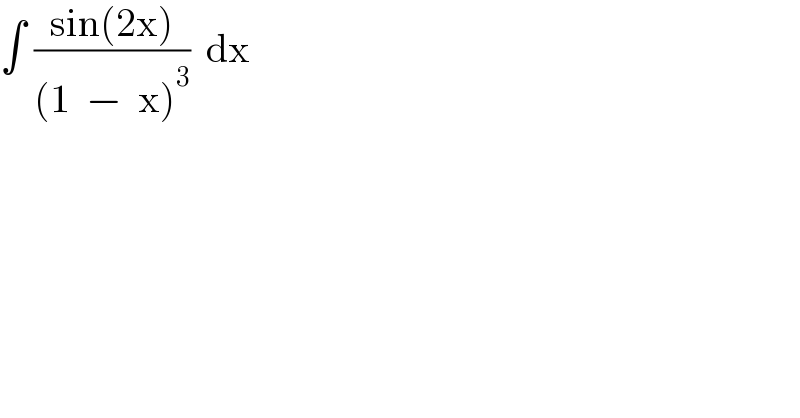
$$\int\:\frac{\mathrm{sin}\left(\mathrm{2x}\right)}{\left(\mathrm{1}\:\:−\:\:\mathrm{x}\right)^{\mathrm{3}} }\:\:\mathrm{dx} \\ $$
Answered by mindispower last updated on 04/Jan/21
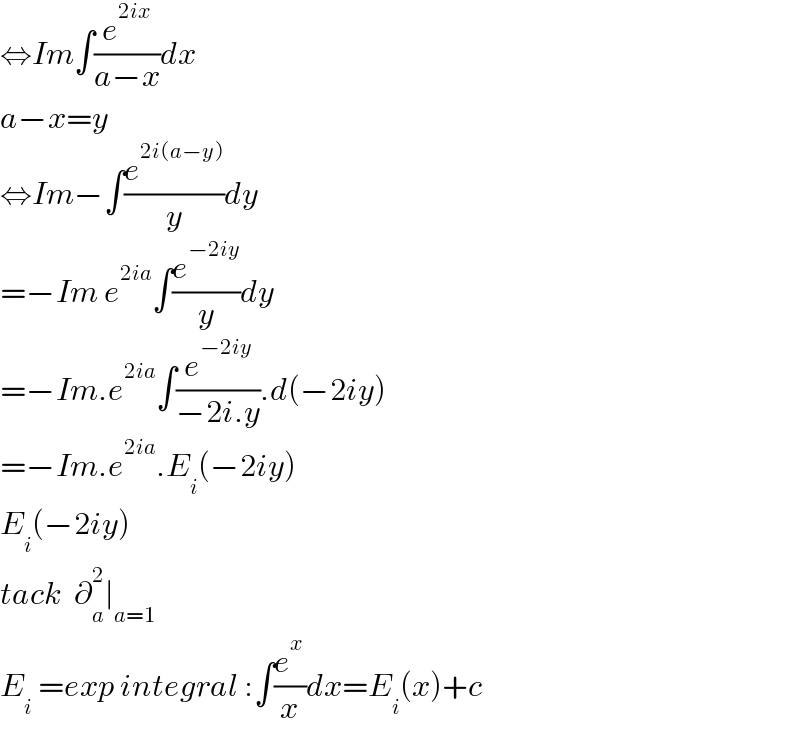
$$\Leftrightarrow{Im}\int\frac{{e}^{\mathrm{2}{ix}} }{{a}−{x}}{dx} \\ $$$${a}−{x}={y} \\ $$$$\Leftrightarrow{Im}−\int\frac{{e}^{\mathrm{2}{i}\left({a}−{y}\right)} }{{y}}{dy} \\ $$$$=−{Im}\:{e}^{\mathrm{2}{ia}} \int\frac{{e}^{−\mathrm{2}{iy}} }{{y}}{dy} \\ $$$$=−{Im}.{e}^{\mathrm{2}{ia}} \int\frac{{e}^{−\mathrm{2}{iy}} }{−\mathrm{2}{i}.{y}}.{d}\left(−\mathrm{2}{iy}\right) \\ $$$$=−{Im}.{e}^{\mathrm{2}{ia}} .{E}_{{i}} \left(−\mathrm{2}{iy}\right) \\ $$$${E}_{{i}} \left(−\mathrm{2}{iy}\right) \\ $$$${tack}\:\:\partial_{{a}} ^{\mathrm{2}} \mid_{{a}=\mathrm{1}} \\ $$$${E}_{{i}} \:={exp}\:{integral}\::\int\frac{{e}^{{x}} }{{x}}{dx}={E}_{{i}} \left({x}\right)+{c} \\ $$
Commented by I want to learn more last updated on 04/Jan/21

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
Commented by mindispower last updated on 04/Jan/21

$${withe}\:{pleasur}\:{sir}\: \\ $$
