Question Number 183156 by cortano1 last updated on 21/Dec/22
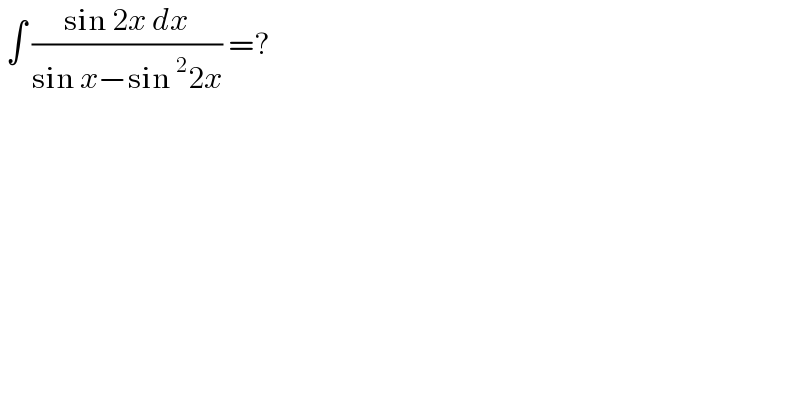
$$\:\int\:\frac{\mathrm{sin}\:\mathrm{2}{x}\:{dx}}{\mathrm{sin}\:{x}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}}\:=? \\ $$
Answered by MJS_new last updated on 21/Dec/22
![∫((sin 2x)/(sin x −sin^2 2x))dx= [t=sin x → dx=(dt/(cos x))] =(1/2)∫(dt/(t^3 −t+(1/4)))=(1/2)∫(dt/((t−α)(t−β)(t−γ))) now use the usual method with α=−((2(√3))/3)sin ((π+arcsin ((3(√3))/8))/3) β=((2(√3))/3)sin ((arcsin ((3(√3))/8))/3) γ=((2(√3))/3)cos ((π+2arcsin ((3(√3))/8))/6)](https://www.tinkutara.com/question/Q183161.png)
$$\int\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{sin}\:{x}\:−\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{sin}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{cos}\:{x}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{{t}^{\mathrm{3}} −{t}+\frac{\mathrm{1}}{\mathrm{4}}}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{\left({t}−\alpha\right)\left({t}−\beta\right)\left({t}−\gamma\right)} \\ $$$$\mathrm{now}\:\mathrm{use}\:\mathrm{the}\:\mathrm{usual}\:\mathrm{method} \\ $$$$\mathrm{with} \\ $$$$\alpha=−\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{sin}\:\frac{\pi+\mathrm{arcsin}\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}}{\mathrm{3}} \\ $$$$\beta=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{sin}\:\frac{\mathrm{arcsin}\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}}{\mathrm{3}} \\ $$$$\gamma=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{cos}\:\frac{\pi+\mathrm{2arcsin}\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}}{\mathrm{6}} \\ $$$$ \\ $$
