Question Number 105854 by bobhans last updated on 01/Aug/20
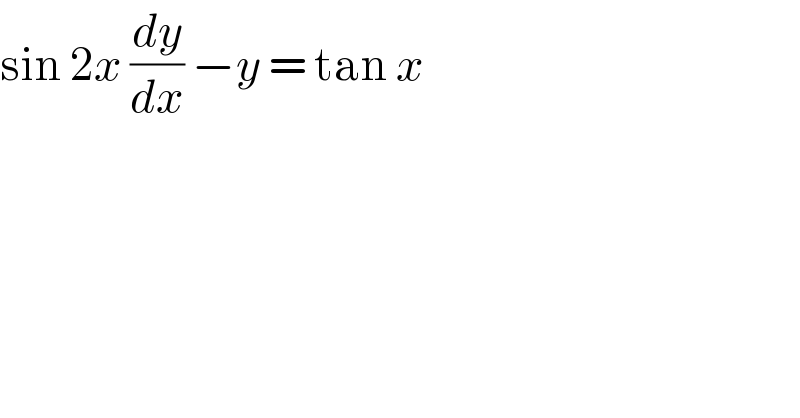
$$\mathrm{sin}\:\mathrm{2}{x}\:\frac{{dy}}{{dx}}\:−{y}\:=\:\mathrm{tan}\:{x} \\ $$
Answered by bemath last updated on 01/Aug/20
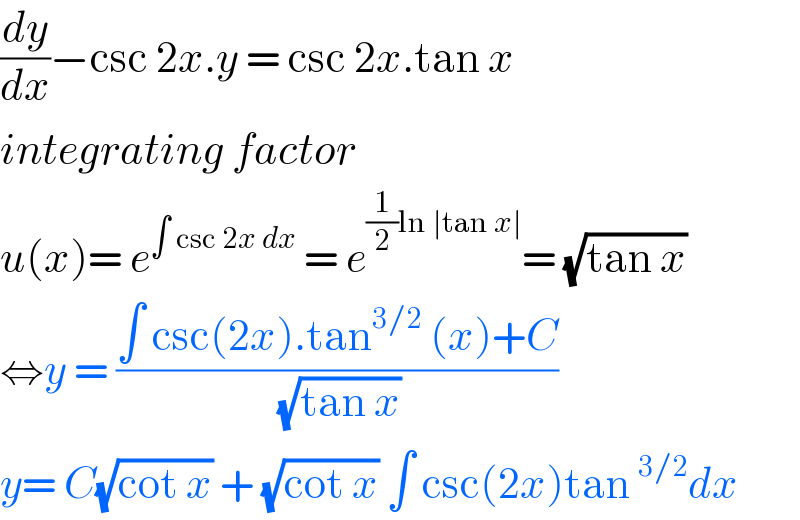
$$\frac{{dy}}{{dx}}−\mathrm{csc}\:\mathrm{2}{x}.{y}\:=\:\mathrm{csc}\:\mathrm{2}{x}.\mathrm{tan}\:{x} \\ $$$${integrating}\:{factor}\: \\ $$$${u}\left({x}\right)=\:{e}^{\int\:\mathrm{csc}\:\mathrm{2}{x}\:{dx}} \:=\:{e}^{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid\mathrm{tan}\:{x}\mid} =\:\sqrt{\mathrm{tan}\:{x}} \\ $$$$\Leftrightarrow{y}\:=\:\frac{\int\:\mathrm{csc}\left(\mathrm{2}{x}\right).\mathrm{tan}^{\mathrm{3}/\mathrm{2}} \:\left({x}\right)+{C}}{\:\sqrt{\mathrm{tan}\:{x}}} \\ $$$${y}=\:{C}\sqrt{\mathrm{cot}\:{x}}\:+\:\sqrt{\mathrm{cot}\:{x}}\:\int\:\mathrm{csc}\left(\mathrm{2}{x}\right)\mathrm{tan}\:^{\mathrm{3}/\mathrm{2}} {dx} \\ $$
Answered by mathmax by abdo last updated on 01/Aug/20

$$\mathrm{sin}\left(\mathrm{2x}\right)×\mathrm{y}^{'} −\mathrm{y}\:=\mathrm{tanx}\:\Rightarrow\mathrm{y}^{'} \:−\frac{\mathrm{1}}{\mathrm{sin}\left(\mathrm{2x}\right)}\mathrm{y}\:=\frac{\mathrm{sinx}}{\mathrm{cosx}}×\frac{\mathrm{1}}{\mathrm{2cosx}\:\mathrm{sinx}} \\ $$$$\Rightarrow\mathrm{y}^{'} \:−\frac{\mathrm{1}}{\mathrm{sin}\left(\mathrm{2x}\right)}\mathrm{y}\:=\frac{\mathrm{1}}{\mathrm{2cos}^{\mathrm{2}} \mathrm{x}}\:\:\left(\mathrm{e}\right) \\ $$$$\mathrm{h}\rightarrow\mathrm{y}^{'} \:=\frac{\mathrm{1}}{\mathrm{sin}\left(\mathrm{2x}\right)}\mathrm{y}\:\Rightarrow\frac{\mathrm{y}^{'} }{\mathrm{y}}\:=\frac{\mathrm{1}}{\mathrm{sin}\left(\mathrm{2x}\right)}\:\Rightarrow\mathrm{ln}\mid\mathrm{y}\mid\:=\int\:\frac{\mathrm{dx}}{\mathrm{sin}\left(\mathrm{2x}\right)} \\ $$$$=_{\mathrm{2x}=\mathrm{t}} \:\:\:\int\:\frac{\mathrm{dt}}{\mathrm{2sint}}\:=_{\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{u}} \:\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{2du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\frac{\mathrm{2u}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int\frac{\mathrm{du}}{\mathrm{u}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{u}\mid\:+\mathrm{c}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)\mid\:+\mathrm{c}\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{tan}\left(\mathrm{x}\right)\mid\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{y}\:=\mathrm{k}\:\sqrt{\mid\mathrm{tanx}\mid}\:\:\mathrm{solution}\:\mathrm{on}\:\left\{\:\mathrm{x}\:/\mathrm{tanx}\:>\mathrm{0}\right\} \\ $$$$\mathrm{mvc}\:\mathrm{method}\:\rightarrow\mathrm{y}^{'} \:=\mathrm{k}^{'} \sqrt{\mathrm{tanx}}\:\:+\mathrm{k}\:×\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}}{\mathrm{2}\sqrt{\mathrm{tanx}}} \\ $$$$\mathrm{e}\:\Rightarrow\mathrm{k}^{'} \sqrt{\mathrm{tanx}}+\mathrm{k}.\frac{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)}{\mathrm{2}\sqrt{\mathrm{tanx}}}−\frac{\mathrm{k}\sqrt{\mathrm{tanx}}}{\mathrm{sin}\left(\mathrm{2x}\right)}=\frac{\mathrm{1}}{\mathrm{2cos}^{\mathrm{2}} \mathrm{x}}\:\Rightarrow \\ $$$$\mathrm{k}^{'} \sqrt{\mathrm{tanx}}+\mathrm{k}\:\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}}{\mathrm{2}\sqrt{\mathrm{tanx}}}−\frac{\mathrm{k}\sqrt{\mathrm{tanx}}}{\frac{\mathrm{2tanx}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}}}\:=\frac{\mathrm{1}}{\mathrm{2cos}^{\mathrm{2}} \mathrm{x}}\:\Rightarrow \\ $$$$\mathrm{k}^{'} \sqrt{\mathrm{tanx}}+\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}\right)\mathrm{k}\left\{\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{tanx}}}−\frac{\sqrt{\mathrm{tanx}}}{\mathrm{2tanx}}\right\}\:=\frac{\mathrm{1}}{\mathrm{2cos}^{\mathrm{2}} \mathrm{x}}\:\Rightarrow \\ $$$$\mathrm{k}^{'} \:=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}}{\:\sqrt{\mathrm{tanx}}}\right)\:\Rightarrow\mathrm{k}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}}{\:\sqrt{\mathrm{tanx}}}\mathrm{dx}\:\:\:\left(\sqrt{\mathrm{tanx}}=\mathrm{t}\:\Rightarrow\mathrm{x}\:=\mathrm{arctan}\left(\mathrm{t}^{\mathrm{2}} \right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{1}+\mathrm{t}^{\mathrm{4}} }{\mathrm{t}}×\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{4}} }\mathrm{dt}\:=\:\int\mathrm{dt}\:=\:\sqrt{\mathrm{tanx}}\:+\lambda\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\left(\sqrt{\mathrm{tanx}}\:+\lambda\right)\sqrt{\mathrm{tanx}}\:=\mathrm{tanx}\:+\lambda\:\sqrt{\mathrm{tanx}} \\ $$$$ \\ $$
