Question Number 109715 by bobhans last updated on 25/Aug/20
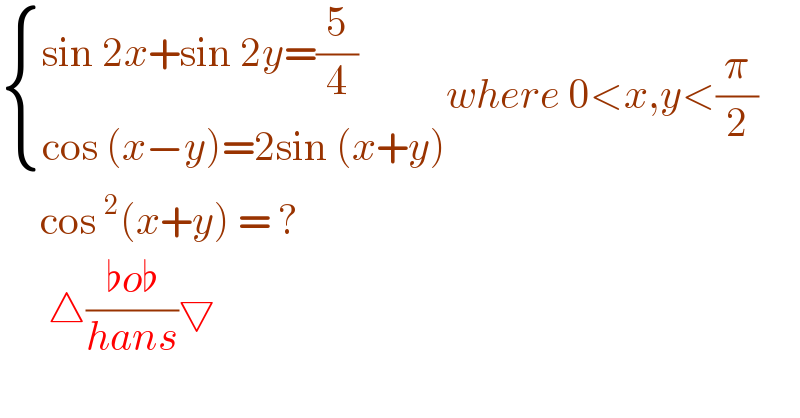
$$\begin{cases}{\mathrm{sin}\:\mathrm{2}{x}+\mathrm{sin}\:\mathrm{2}{y}=\frac{\mathrm{5}}{\mathrm{4}}}\\{\mathrm{cos}\:\left({x}−{y}\right)=\mathrm{2sin}\:\left({x}+{y}\right)}\end{cases}{where}\:\mathrm{0}<{x},{y}<\frac{\pi}{\mathrm{2}} \\ $$$$\:\:\:\:\:\mathrm{cos}\:^{\mathrm{2}} \left({x}+{y}\right)\:=\:? \\ $$$$\:\:\:\:\:\:\bigtriangleup\frac{\flat{o}\flat}{{hans}}\bigtriangledown \\ $$
Answered by nimnim last updated on 25/Aug/20
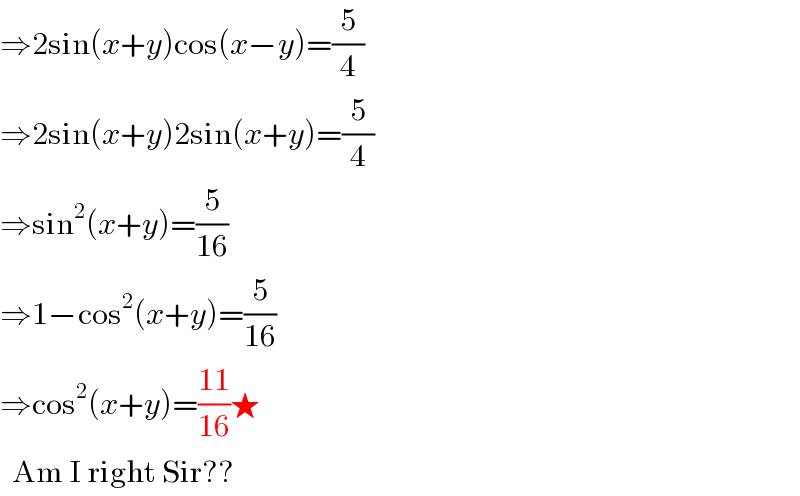
$$\Rightarrow\mathrm{2sin}\left({x}+{y}\right)\mathrm{cos}\left({x}−{y}\right)=\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{2sin}\left({x}+{y}\right)\mathrm{2sin}\left({x}+{y}\right)=\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{sin}^{\mathrm{2}} \left({x}+{y}\right)=\frac{\mathrm{5}}{\mathrm{16}} \\ $$$$\Rightarrow\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \left({x}+{y}\right)=\frac{\mathrm{5}}{\mathrm{16}} \\ $$$$\Rightarrow\mathrm{cos}^{\mathrm{2}} \left({x}+{y}\right)=\frac{\mathrm{11}}{\mathrm{16}}\bigstar \\ $$$$\:\:\mathrm{Am}\:\mathrm{I}\:\mathrm{right}\:\mathrm{Sir}?? \\ $$
Commented by bobhans last updated on 25/Aug/20

$${good}….{santuyy} \\ $$
