Menu Close

sin-3-x-1-sin-2-x-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 167312 by cortano1 last updated on 12/Mar/22
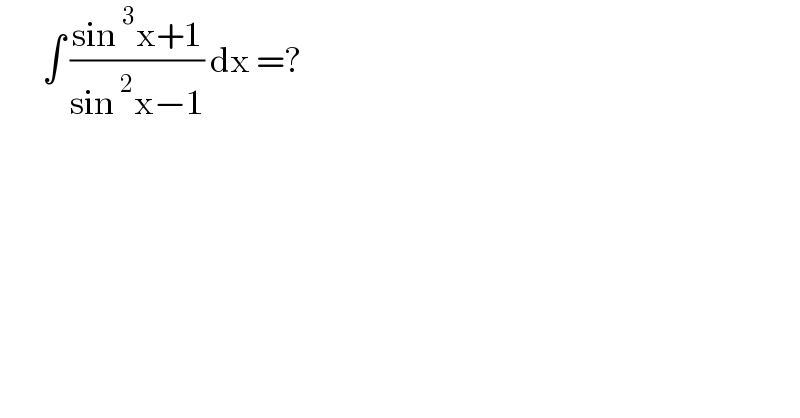
∫ ((sin^3 x+1)/(sin^2 x−1)) dx =?
$$\:\:\:\:\:\:\:\int\:\frac{\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}+\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}−\mathrm{1}}\:\mathrm{dx}\:=? \\ $$
Commented by Florian last updated on 10/Apr/22
Simplify: ((sin^3 x+1)/(sin^2 −1))=((sin^2 (x)−sin(x)+1)/(sin(x)−1)) =∫((sin^2 (x))/(sin(x)−1))dx−∫((sin(x))/(sin(x)−1))dx+∫(1/(sin(x)−1))dx ∫((sin^2 (x))/(sin(x)−1))dx=(2/(tan((x/2))−1))−cos(x)+x ∫((sin(x))/(sin(x)−1))dx=−4(−(1/(2(tan((x/2))−1)))−(1/2)arctan(tan((x/2)))) ∫(1/(sin(x)−1))dx=2((1/((−1+tan((x/2)))^2 ))+(2/(−1+tan((x/2))))+((tan((x/2)))/(2tan((x/2))+sec^2 ((x/2))))) =x+(4/(tan((x/2))−1))−cos(x)−2arctan(tan((x/2)))+(2/((tan((x/2))−1)^2 ))+((2tan((x/2)))/(2tan((x/2))−sec^2 ((x/2))))+c, c∈R
$$\:\:{Simplify}:\:\frac{{sin}^{\mathrm{3}} {x}+\mathrm{1}}{{sin}^{\mathrm{2}} −\mathrm{1}}=\frac{{sin}^{\mathrm{2}} \left({x}\right)−{sin}\left({x}\right)+\mathrm{1}}{{sin}\left({x}\right)−\mathrm{1}} \\ $$$$=\int\frac{{sin}^{\mathrm{2}} \left({x}\right)}{{sin}\left({x}\right)−\mathrm{1}}{dx}−\int\frac{{sin}\left({x}\right)}{{sin}\left({x}\right)−\mathrm{1}}{dx}+\int\frac{\mathrm{1}}{{sin}\left({x}\right)−\mathrm{1}}{dx} \\ $$$$\int\frac{{sin}^{\mathrm{2}} \left({x}\right)}{{sin}\left({x}\right)−\mathrm{1}}{dx}=\frac{\mathrm{2}}{{tan}\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{1}}−{cos}\left({x}\right)+{x} \\ $$$$\int\frac{{sin}\left({x}\right)}{{sin}\left({x}\right)−\mathrm{1}}{dx}=−\mathrm{4}\left(−\frac{\mathrm{1}}{\mathrm{2}\left({tan}\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left({tan}\left(\frac{{x}}{\mathrm{2}}\right)\right)\right) \\ $$$$\int\frac{\mathrm{1}}{{sin}\left({x}\right)−\mathrm{1}}{dx}=\mathrm{2}\left(\frac{\mathrm{1}}{\left(−\mathrm{1}+{tan}\left(\frac{{x}}{\mathrm{2}}\right)\right)^{\mathrm{2}} }+\frac{\mathrm{2}}{−\mathrm{1}+{tan}\left(\frac{{x}}{\mathrm{2}}\right)}+\frac{{tan}\left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}{tan}\left(\frac{{x}}{\mathrm{2}}\right)+{sec}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}\right) \\ $$$$={x}+\frac{\mathrm{4}}{{tan}\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{1}}−{cos}\left({x}\right)−\mathrm{2}{arctan}\left({tan}\left(\frac{{x}}{\mathrm{2}}\right)\right)+\frac{\mathrm{2}}{\left({tan}\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{2}{tan}\left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}{tan}\left(\frac{{x}}{\mathrm{2}}\right)−{sec}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}+{c},\:{c}\in{R} \\ $$
Answered by MJS_new last updated on 12/Mar/22
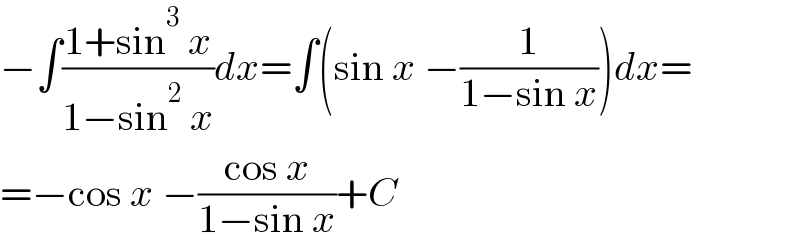
−∫((1+sin^3 x)/(1−sin^2 x))dx=∫(sin x −(1/(1−sin x)))dx= =−cos x −((cos x)/(1−sin x))+C
$$−\int\frac{\mathrm{1}+\mathrm{sin}^{\mathrm{3}} \:{x}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{x}}{dx}=\int\left(\mathrm{sin}\:{x}\:−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}\:{x}}\right){dx}= \\ $$$$=−\mathrm{cos}\:{x}\:−\frac{\mathrm{cos}\:{x}}{\mathrm{1}−\mathrm{sin}\:{x}}+{C} \\ $$
Commented by cortano1 last updated on 13/Mar/22
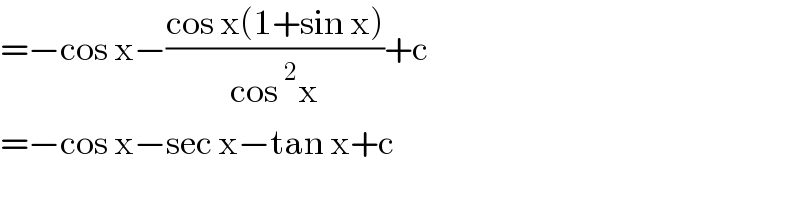
=−cos x−((cos x(1+sin x))/(cos^2 x))+c =−cos x−sec x−tan x+c
$$=−\mathrm{cos}\:\mathrm{x}−\frac{\mathrm{cos}\:\mathrm{x}\left(\mathrm{1}+\mathrm{sin}\:\mathrm{x}\right)}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}+\mathrm{c} \\ $$$$=−\mathrm{cos}\:\mathrm{x}−\mathrm{sec}\:\mathrm{x}−\mathrm{tan}\:\mathrm{x}+\mathrm{c} \\ $$
Answered by LEKOUMA last updated on 13/Mar/22
=∫(((sin x+1)(sin^2 x−sin x+1))/((sin x−1)(sin x+1)))dx =∫((sin^2 x−sin x+1)/(sin x−1))dx =∫((sin^2 x−sin x)/(sin x−1))dx+∫(1/(sin x−1))dx =∫((sin x(sin x−1))/((sin x−1)))dx+∫(1/(sin x−1))dx =∫sin xdx+∫(1/(sin x−1))dx =−cos x+∫(1/(sin x−1))dx ∫(1/(sin x−1))dx sin x=((2tan ((x/2)))/(1+tan^2 ((x/2)))) ∫(1/(((2tan ((x/2)))/(1+tan^2 ((x/2))))−1))dx let t=tan ((x/2)) ⇒ dt=(1/2)(1+tan^2 ((x/2)))dx ∫(1/(((2t)/(1+t^2 ))−1))×(dt/((1/2)(1+t^2 ))) ∫(1/((2t−1−t^2 )/(1+t^2 )))×(dt/((1/2)(1+t^2 ))) ∫((1+t^2 )/(2t−1−t^2 ))×(dt/((1/2)(1+t^2 ))) (1/2)∫(1/(2t−1−t^2 ))dt=(1/2)∫(1/(−t^2 +2t−1 ))dt (1/2)∫(1/(−t^2 +2t−1))dt=−(1/2)∫(1/(t^2 −2t+1))dt −(1/2)∫(1/((t−1)^2 +(3/4)))dt let u=t−1⇒ du=dt −(1/2)∫(1/(u^2 +(3/4)))du=−(1/2)∫(1/(u^2 +(((√3)/2))^2 ))du =−(1/2)(1/((√3)/2))tan^(−1) ((u/((√3)/2)))+c, c∈ lR =−(√3)tan^(−1) (((2u)/( (√3))))+c, c∈R =−(√3)tan^(−1) (((2(√3))/3)u)+ c, c∈lR =−(√3)tan^(−1) [((2(√3))/3)(t−1)]+c, c∈R =(√3)tan^(−1) [((2(√3))/3)(tan ((x/2))−1)]+c, c∈lR ∫(1/(sin x−1))dx=(√3)tan^(−1) [((2(√3))/3)(tan ((x/2))−1)]+c, c∈lR =−cos x+(√3)tan^(−1) [((2(√3))/3)(tan ((x/2))−1)]+c, c∈lR ∫((sin^3 x+1)/(sin^2 x−1))dx=−cos x+(√3)tan^(−1) [((2(√3))/3)(tan ((x/2))−1)]+c, c∈lR Proposition
$$=\int\frac{\left(\mathrm{sin}\:{x}+\mathrm{1}\right)\left(\mathrm{sin}\:^{\mathrm{2}} {x}−\mathrm{sin}\:{x}+\mathrm{1}\right)}{\left(\mathrm{sin}\:{x}−\mathrm{1}\right)\left(\mathrm{sin}\:{x}+\mathrm{1}\right)}{dx} \\ $$$$=\int\frac{\mathrm{sin}\:^{\mathrm{2}} {x}−\mathrm{sin}\:{x}+\mathrm{1}}{\mathrm{sin}\:{x}−\mathrm{1}}{dx} \\ $$$$=\int\frac{\mathrm{sin}\:^{\mathrm{2}} {x}−\mathrm{sin}\:{x}}{\mathrm{sin}\:{x}−\mathrm{1}}{dx}+\int\frac{\mathrm{1}}{\mathrm{sin}\:{x}−\mathrm{1}}{dx} \\ $$$$=\int\frac{\mathrm{sin}\:{x}\left(\mathrm{sin}\:{x}−\mathrm{1}\right)}{\left(\mathrm{sin}\:{x}−\mathrm{1}\right)}{dx}+\int\frac{\mathrm{1}}{\mathrm{sin}\:{x}−\mathrm{1}}{dx} \\ $$$$=\int\mathrm{sin}\:{xdx}+\int\frac{\mathrm{1}}{\mathrm{sin}\:{x}−\mathrm{1}}{dx} \\ $$$$=−\mathrm{cos}\:{x}+\int\frac{\mathrm{1}}{\mathrm{sin}\:{x}−\mathrm{1}}{dx} \\ $$$$\int\frac{\mathrm{1}}{\mathrm{sin}\:{x}−\mathrm{1}}{dx} \\ $$$$\mathrm{sin}\:{x}=\frac{\mathrm{2tan}\:\left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$$\int\frac{\mathrm{1}}{\frac{\mathrm{2tan}\:\left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}−\mathrm{1}}{dx} \\ $$$${let}\:{t}=\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)\:\Rightarrow\:{dt}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right){dx} \\ $$$$\int\frac{\mathrm{1}}{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }−\mathrm{1}}×\frac{{dt}}{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$$\int\frac{\mathrm{1}}{\frac{\mathrm{2}{t}−\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}×\frac{{dt}}{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$$\int\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{2}{t}−\mathrm{1}−{t}^{\mathrm{2}} }×\frac{{dt}}{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{\mathrm{2}{t}−\mathrm{1}−{t}^{\mathrm{2}} }{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{−{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}\:}{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{−{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}}{dt}=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}}{dt} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}{dt} \\ $$$${let}\:{u}={t}−\mathrm{1}\Rightarrow\:{du}={dt} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{{u}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}{du}=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{{u}^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }{du} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\frac{\mathrm{1}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{{u}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\right)+{c},\:{c}\in\:{lR} \\ $$$$=−\sqrt{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{u}}{\:\sqrt{\mathrm{3}}}\right)+{c},\:{c}\in{R} \\ $$$$=−\sqrt{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}{u}\right)+\:{c},\:{c}\in{lR} \\ $$$$=−\sqrt{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \left[\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\left({t}−\mathrm{1}\right)\right]+{c},\:{c}\in{R} \\ $$$$=\sqrt{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \left[\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{1}\right)\right]+{c},\:{c}\in{lR} \\ $$$$\int\frac{\mathrm{1}}{\mathrm{sin}\:{x}−\mathrm{1}}{dx}=\sqrt{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \left[\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{1}\right)\right]+{c},\:{c}\in{lR} \\ $$$$=−\mathrm{cos}\:{x}+\sqrt{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \left[\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{1}\right)\right]+{c},\:{c}\in{lR} \\ $$$$\int\frac{\mathrm{sin}\:^{\mathrm{3}} {x}+\mathrm{1}}{\mathrm{sin}\:^{\mathrm{2}} {x}−\mathrm{1}}{dx}=−\mathrm{cos}\:{x}+\sqrt{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \left[\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{1}\right)\right]+{c},\:{c}\in{lR} \\ $$$${Proposition} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *