Question Number 166796 by cortano1 last updated on 28/Feb/22
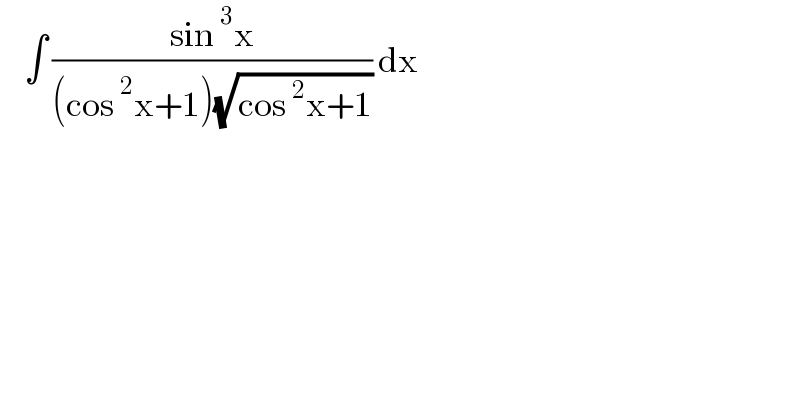
$$\:\:\:\:\int\:\frac{\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}}{\left(\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}+\mathrm{1}}}\:\mathrm{dx} \\ $$
Answered by MJS_new last updated on 28/Feb/22
![∫((sin^3 x)/((1+cos^2 x)^(3/2) ))dx= [t=cos x → dx=−(dt/(sin x))] =∫((t^2 −1)/((t^2 +1)^(3/2) ))dt= [u=t+(√(t^2 +1)) → dt=((√(t^2 +1))/u)du] =∫((u^4 −6u^2 +1)/(u(u^2 +1)^2 ))du=∫((1/u)−((8u)/((u^2 +1)^2 )))du= =ln u +(4/(u^2 +1))= =ln (t+(√(t^2 +1))) −((2t)/( (√(t^2 +1))))= =ln (cos x +(√(1+cos^2 x))) −((2cos x)/( (√(1+cos^2 x))))+C](https://www.tinkutara.com/question/Q166803.png)
$$\int\frac{\mathrm{sin}^{\mathrm{3}} \:{x}}{\left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:{x}\right)^{\mathrm{3}/\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{cos}\:{x}\:\rightarrow\:{dx}=−\frac{{dt}}{\mathrm{sin}\:{x}}\right] \\ $$$$=\int\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} }{dt}= \\ $$$$\:\:\:\:\:\left[{u}={t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\:\rightarrow\:{dt}=\frac{\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{{u}}{du}\right] \\ $$$$=\int\frac{{u}^{\mathrm{4}} −\mathrm{6}{u}^{\mathrm{2}} +\mathrm{1}}{{u}\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{du}=\int\left(\frac{\mathrm{1}}{{u}}−\frac{\mathrm{8}{u}}{\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\right){du}= \\ $$$$=\mathrm{ln}\:{u}\:+\frac{\mathrm{4}}{{u}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$=\mathrm{ln}\:\left({t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\right)\:−\frac{\mathrm{2}{t}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}= \\ $$$$=\mathrm{ln}\:\left(\mathrm{cos}\:{x}\:+\sqrt{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:{x}}\right)\:−\frac{\mathrm{2cos}\:{x}}{\:\sqrt{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:{x}}}+{C} \\ $$
Commented by peter frank last updated on 28/Feb/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
