Question Number 144829 by mathlove last updated on 29/Jun/21
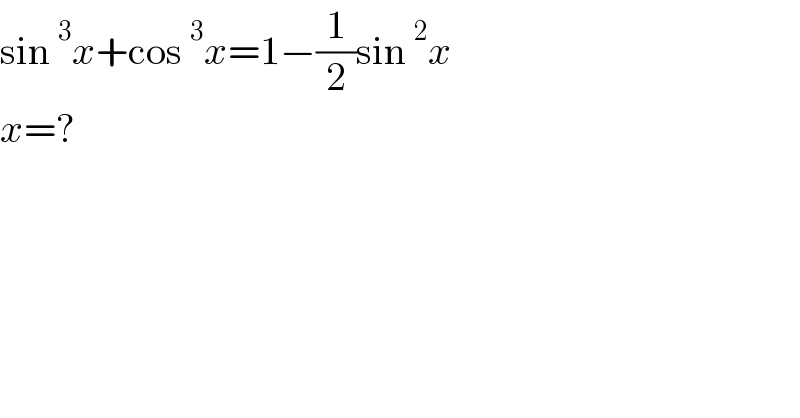
$$\mathrm{sin}\:^{\mathrm{3}} {x}+\mathrm{cos}\:^{\mathrm{3}} {x}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} {x} \\ $$$${x}=? \\ $$
Answered by ajfour last updated on 29/Jun/21
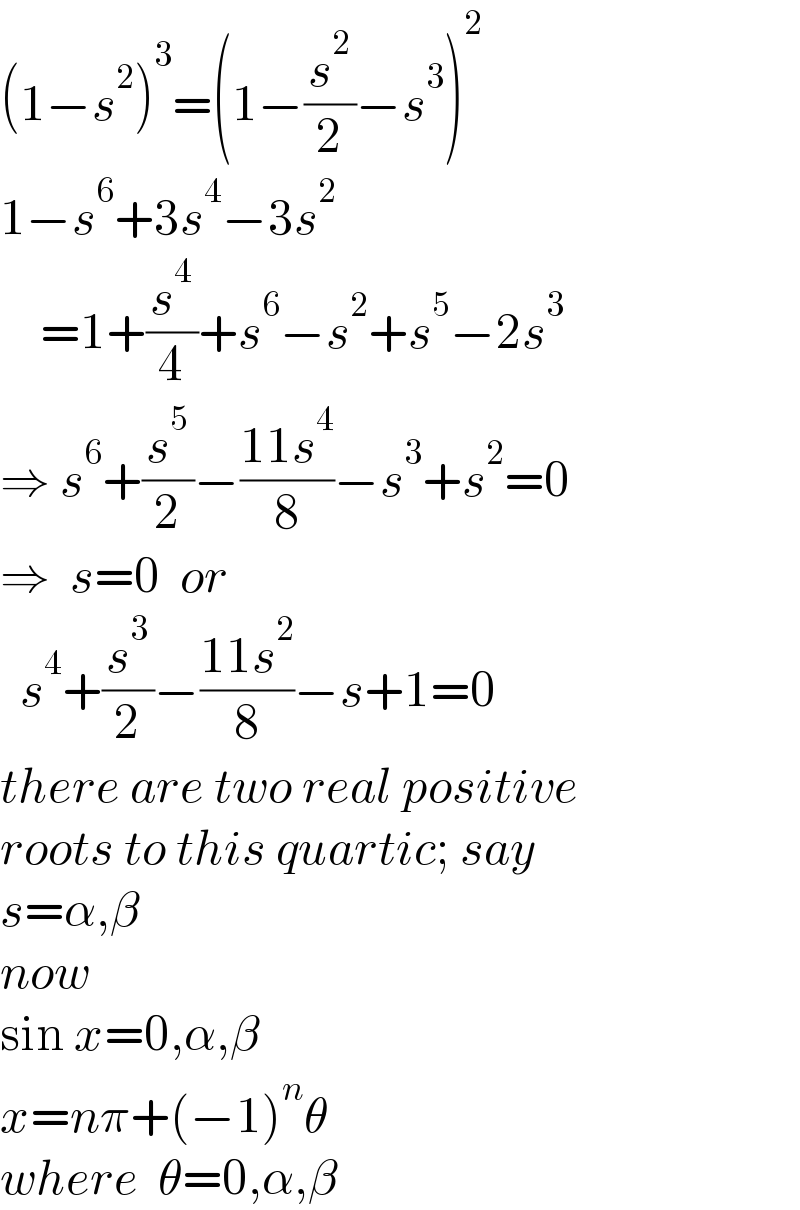
$$\left(\mathrm{1}−{s}^{\mathrm{2}} \right)^{\mathrm{3}} =\left(\mathrm{1}−\frac{{s}^{\mathrm{2}} }{\mathrm{2}}−{s}^{\mathrm{3}} \right)^{\mathrm{2}} \\ $$$$\mathrm{1}−{s}^{\mathrm{6}} +\mathrm{3}{s}^{\mathrm{4}} −\mathrm{3}{s}^{\mathrm{2}} \\ $$$$\:\:\:\:=\mathrm{1}+\frac{{s}^{\mathrm{4}} }{\mathrm{4}}+{s}^{\mathrm{6}} −{s}^{\mathrm{2}} +{s}^{\mathrm{5}} −\mathrm{2}{s}^{\mathrm{3}} \\ $$$$\Rightarrow\:{s}^{\mathrm{6}} +\frac{{s}^{\mathrm{5}} }{\mathrm{2}}−\frac{\mathrm{11}{s}^{\mathrm{4}} }{\mathrm{8}}−{s}^{\mathrm{3}} +{s}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:\:{s}=\mathrm{0}\:\:{or} \\ $$$$\:\:{s}^{\mathrm{4}} +\frac{{s}^{\mathrm{3}} }{\mathrm{2}}−\frac{\mathrm{11}{s}^{\mathrm{2}} }{\mathrm{8}}−{s}+\mathrm{1}=\mathrm{0} \\ $$$${there}\:{are}\:{two}\:{real}\:{positive} \\ $$$${roots}\:{to}\:{this}\:{quartic};\:{say} \\ $$$${s}=\alpha,\beta \\ $$$${now} \\ $$$$\mathrm{sin}\:{x}=\mathrm{0},\alpha,\beta \\ $$$${x}={n}\pi+\left(−\mathrm{1}\right)^{{n}} \theta \\ $$$${where}\:\:\theta=\mathrm{0},\alpha,\beta \\ $$
Answered by liberty last updated on 29/Jun/21
![sin^3 x+cos^3 x=sin^2 x+cos^2 x−(1/2)sin^2 x sin^3 x+cos^3 x=(1/2)sin^2 x+cos^2 x cos^3 x−cos^2 x=(1/2)sin^2 x−sin^3 x cos^2 x(cos x−1)=sin^2 x((1/2)−sin x) cos^2 x(−2sin^2 (1/2)x)=sin^2 x((1/2)−2sin (1/2)xcos (1/2)x) let tan (x/2)=t⇒tan x=((2t)/(1−t^2 )) ⇒−2((t^2 /(1+t^2 )))=(((2t)/(1−t^2 )))((1/2)−((2t)/(1+t^2 ))) ⇒((−2t^2 )/(1+t^2 ))= (((2t)/(1−t^2 )))(((1+t^2 −4t)/(2(1+t^2 )))) ⇒(((2t)/(1+t^2 )))[((t^2 −4t+1)/(2−2t^2 )) +t ]=0 ⇒(((2t)/(1+t^2 )))[((t^2 −4t+1+2t−2t^3 )/(2−2t^2 ))]=0 ⇒(((2t)/(1+t^2 )))(((2t^3 −t^2 +2t−1)/(2−2t^2 )))=0 we get t=0 ⇒tan (x/2) = 0 →(x/2) = 0+kπ ⇒x= 2kπ ; k∈Z for 2t^3 −t^2 +2t−1=0 test t=(1/2)→(1/4)−(1/4)+1−1=0 (valid) ⇒factorise (2t−1)(t^2 +1)=0 ⇒tan (x/2)=(1/2) ; (x/2)= arctan ((1/2))+kπ ⇒x=2arctan ((1/2))+2kπ](https://www.tinkutara.com/question/Q144834.png)
$$\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}=\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} \mathrm{x} \\ $$$$\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{x} \\ $$$$\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}−\mathrm{sin}\:^{\mathrm{3}} \mathrm{x} \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\left(\mathrm{cos}\:\mathrm{x}−\mathrm{1}\right)=\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{sin}\:\mathrm{x}\right) \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\left(−\mathrm{2sin}\:^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)=\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2sin}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{xcos}\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right) \\ $$$$\mathrm{let}\:\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}}=\mathrm{t}\Rightarrow\mathrm{tan}\:\mathrm{x}=\frac{\mathrm{2t}}{\mathrm{1}−\mathrm{t}^{\mathrm{2}} } \\ $$$$\Rightarrow−\mathrm{2}\left(\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)=\left(\frac{\mathrm{2t}}{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\right)\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\frac{−\mathrm{2t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }=\:\left(\frac{\mathrm{2t}}{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\right)\left(\frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} −\mathrm{4t}}{\mathrm{2}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\right) \\ $$$$\Rightarrow\left(\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)\left[\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{4t}+\mathrm{1}}{\mathrm{2}−\mathrm{2t}^{\mathrm{2}} }\:+\mathrm{t}\:\right]=\mathrm{0} \\ $$$$\Rightarrow\left(\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)\left[\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{4t}+\mathrm{1}+\mathrm{2t}−\mathrm{2t}^{\mathrm{3}} }{\mathrm{2}−\mathrm{2t}^{\mathrm{2}} }\right]=\mathrm{0} \\ $$$$\Rightarrow\left(\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)\left(\frac{\mathrm{2t}^{\mathrm{3}} −\mathrm{t}^{\mathrm{2}} +\mathrm{2t}−\mathrm{1}}{\mathrm{2}−\mathrm{2t}^{\mathrm{2}} }\right)=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{t}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}}\:=\:\mathrm{0}\:\rightarrow\frac{\mathrm{x}}{\mathrm{2}}\:=\:\mathrm{0}+\mathrm{k}\pi \\ $$$$\Rightarrow\mathrm{x}=\:\mathrm{2k}\pi\:;\:\mathrm{k}\in\mathbb{Z}\:\: \\ $$$$\mathrm{for}\:\mathrm{2t}^{\mathrm{3}} −\mathrm{t}^{\mathrm{2}} +\mathrm{2t}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{test}\:\mathrm{t}=\frac{\mathrm{1}}{\mathrm{2}}\rightarrow\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{1}−\mathrm{1}=\mathrm{0}\:\left(\mathrm{valid}\right) \\ $$$$\Rightarrow\mathrm{factorise}\:\left(\mathrm{2t}−\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\:;\:\frac{\mathrm{x}}{\mathrm{2}}=\:\mathrm{arctan}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{k}\pi \\ $$$$\Rightarrow\mathrm{x}=\mathrm{2arctan}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{2k}\pi \\ $$
