Menu Close

sin-3-x-cos-3-x-sin-x-cos-x-1-Find-x-

Tinku Tara 0 Comments
Pin




Question Number 128743 by bemath last updated on 10/Jan/21
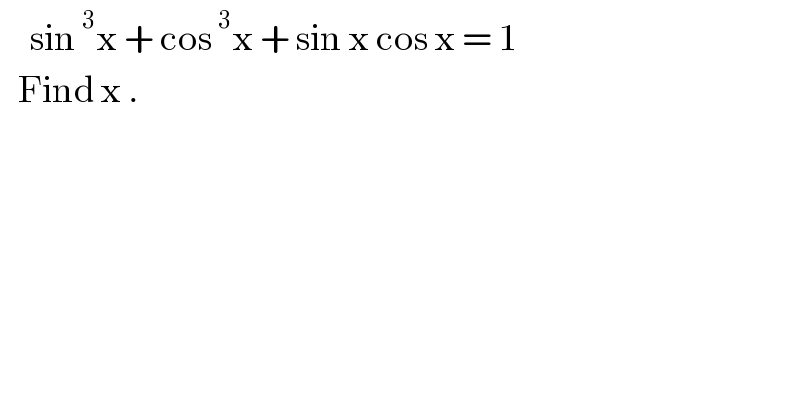
sin^3 x + cos^3 x + sin x cos x = 1 Find x .
$$\:\:\:\:\:\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}\:+\:\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}\:+\:\mathrm{sin}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{x}\:=\:\mathrm{1} \\ $$$$\:\:\:\mathrm{Find}\:\mathrm{x}\:. \\ $$
Answered by liberty last updated on 10/Jan/21
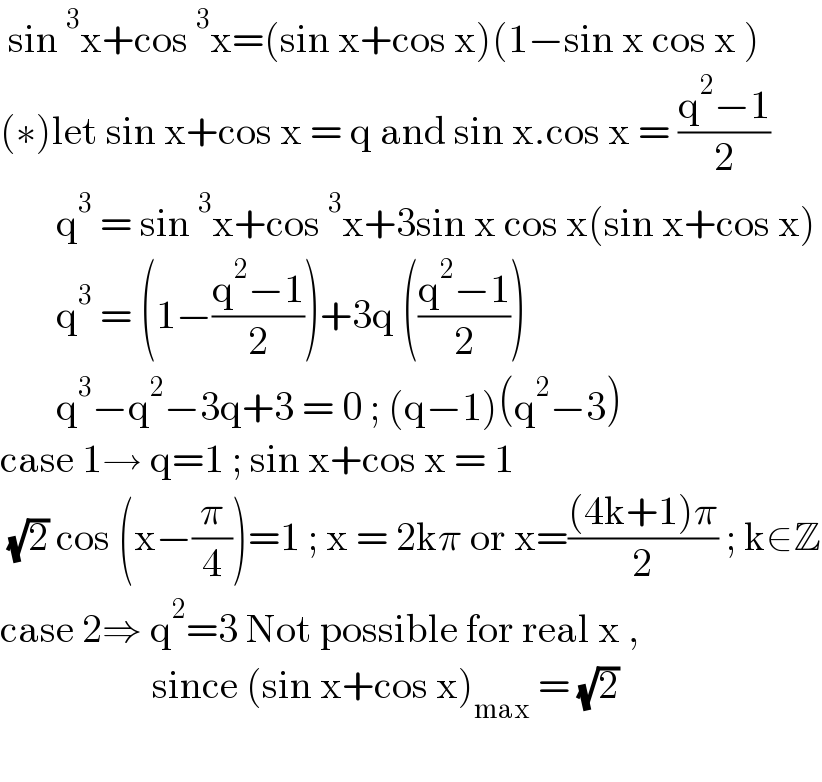
sin^3 x+cos^3 x=(sin x+cos x)(1−sin x cos x ) (∗)let sin x+cos x = q and sin x.cos x = ((q^2 −1)/2) q^3 = sin^3 x+cos^3 x+3sin x cos x(sin x+cos x) q^3 = (1−((q^2 −1)/2))+3q (((q^2 −1)/2)) q^3 −q^2 −3q+3 = 0 ; (q−1)(q^2 −3) case 1→ q=1 ; sin x+cos x = 1 (√2) cos (x−(π/4))=1 ; x = 2kπ or x=(((4k+1)π)/2) ; k∈Z case 2⇒ q^2 =3 Not possible for real x , since (sin x+cos x)_(max) = (√2)
$$\:\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}=\left(\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\right)\left(\mathrm{1}−\mathrm{sin}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{x}\:\right) \\ $$$$\left(\ast\right)\mathrm{let}\:\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\:=\:\mathrm{q}\:\mathrm{and}\:\mathrm{sin}\:\mathrm{x}.\mathrm{cos}\:\mathrm{x}\:=\:\frac{\mathrm{q}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\mathrm{q}^{\mathrm{3}} \:=\:\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}+\mathrm{3sin}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{x}\left(\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{q}^{\mathrm{3}} \:=\:\left(\mathrm{1}−\frac{\mathrm{q}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}\right)+\mathrm{3q}\:\left(\frac{\mathrm{q}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{q}^{\mathrm{3}} −\mathrm{q}^{\mathrm{2}} −\mathrm{3q}+\mathrm{3}\:=\:\mathrm{0}\:;\:\left(\mathrm{q}−\mathrm{1}\right)\left(\mathrm{q}^{\mathrm{2}} −\mathrm{3}\right) \\ $$$$\mathrm{case}\:\mathrm{1}\rightarrow\:\mathrm{q}=\mathrm{1}\:;\:\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\:=\:\mathrm{1}\: \\ $$$$\:\sqrt{\mathrm{2}}\:\mathrm{cos}\:\left(\mathrm{x}−\frac{\pi}{\mathrm{4}}\right)=\mathrm{1}\:;\:\mathrm{x}\:=\:\mathrm{2k}\pi\:\mathrm{or}\:\mathrm{x}=\frac{\left(\mathrm{4k}+\mathrm{1}\right)\pi}{\mathrm{2}}\:;\:\mathrm{k}\in\mathbb{Z} \\ $$$$\mathrm{case}\:\mathrm{2}\Rightarrow\:\mathrm{q}^{\mathrm{2}} =\mathrm{3}\:\mathrm{Not}\:\mathrm{possible}\:\mathrm{for}\:\mathrm{real}\:\mathrm{x}\:,\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{since}\:\left(\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\right)_{\mathrm{max}} \:=\:\sqrt{\mathrm{2}}\: \\ $$$$ \\ $$
Answered by MJS_new last updated on 10/Jan/21
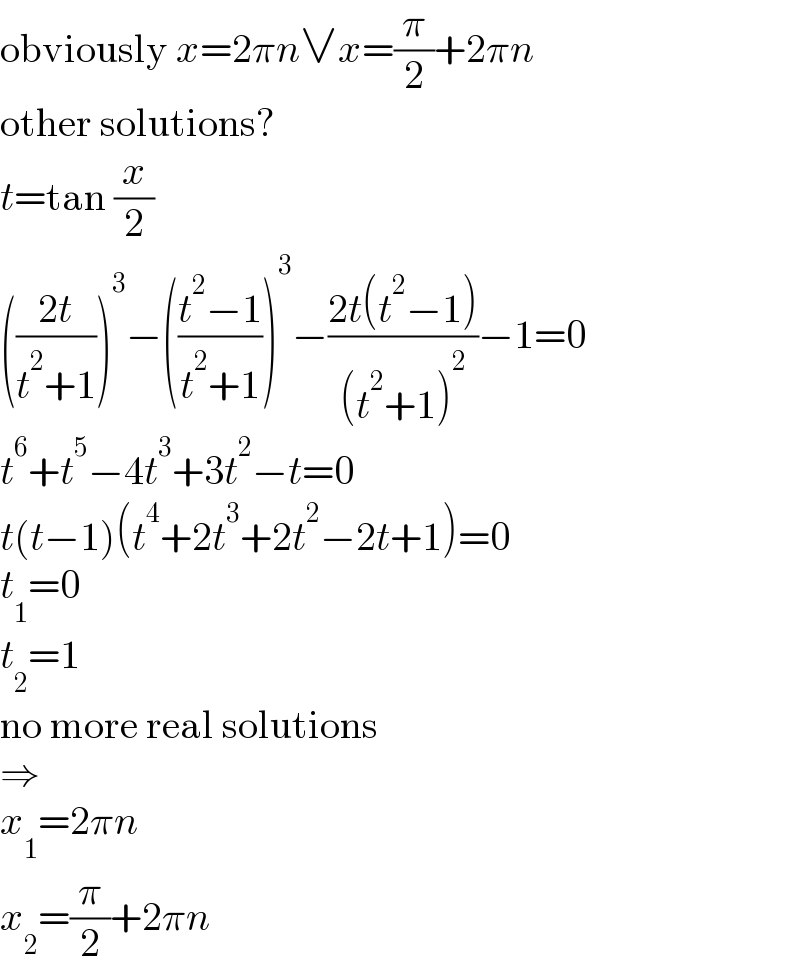
obviously x=2πn∨x=(π/2)+2πn other solutions? t=tan (x/2) (((2t)/(t^2 +1)))^3 −(((t^2 −1)/(t^2 +1)))^3 −((2t(t^2 −1))/((t^2 +1)^2 ))−1=0 t^6 +t^5 −4t^3 +3t^2 −t=0 t(t−1)(t^4 +2t^3 +2t^2 −2t+1)=0 t_1 =0 t_2 =1 no more real solutions ⇒ x_1 =2πn x_2 =(π/2)+2πn
$$\mathrm{obviously}\:{x}=\mathrm{2}\pi{n}\vee{x}=\frac{\pi}{\mathrm{2}}+\mathrm{2}\pi{n} \\ $$$$\mathrm{other}\:\mathrm{solutions}? \\ $$$${t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}} \\ $$$$\left(\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{3}} −\left(\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{3}} −\frac{\mathrm{2}{t}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }−\mathrm{1}=\mathrm{0} \\ $$$${t}^{\mathrm{6}} +{t}^{\mathrm{5}} −\mathrm{4}{t}^{\mathrm{3}} +\mathrm{3}{t}^{\mathrm{2}} −{t}=\mathrm{0} \\ $$$${t}\left({t}−\mathrm{1}\right)\left({t}^{\mathrm{4}} +\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}\right)=\mathrm{0} \\ $$$${t}_{\mathrm{1}} =\mathrm{0} \\ $$$${t}_{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{no}\:\mathrm{more}\:\mathrm{real}\:\mathrm{solutions} \\ $$$$\Rightarrow \\ $$$${x}_{\mathrm{1}} =\mathrm{2}\pi{n} \\ $$$${x}_{\mathrm{2}} =\frac{\pi}{\mathrm{2}}+\mathrm{2}\pi{n} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *