Menu Close

sin-3-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 43861 by Tinkutara last updated on 16/Sep/18
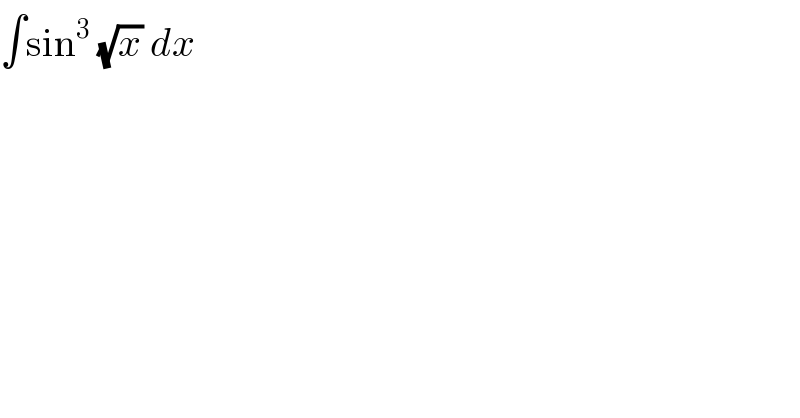
∫sin^3 (√x) dx
$$\int\mathrm{sin}^{\mathrm{3}} \:\sqrt{{x}}\:{dx} \\ $$
Commented by Tinkutara last updated on 16/Sep/18
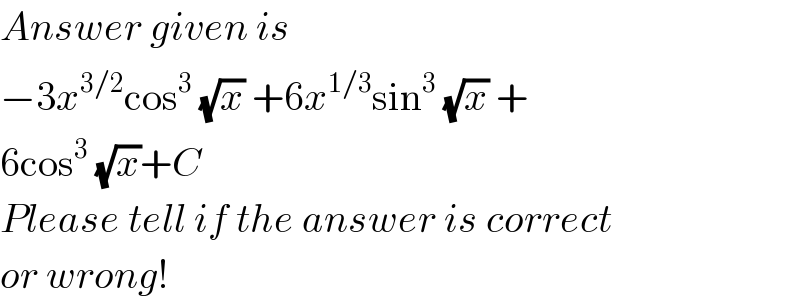
Answer given is −3x^(3/2) cos^3 (√x) +6x^(1/3) sin^3 (√x) + 6cos^3 (√x)+C Please tell if the answer is correct or wrong!
$${Answer}\:{given}\:{is} \\ $$$$−\mathrm{3}{x}^{\mathrm{3}/\mathrm{2}} \mathrm{cos}^{\mathrm{3}} \:\sqrt{{x}}\:+\mathrm{6}{x}^{\mathrm{1}/\mathrm{3}} \mathrm{sin}^{\mathrm{3}} \:\sqrt{{x}}\:+ \\ $$$$\mathrm{6cos}^{\mathrm{3}} \:\sqrt{{x}}+{C} \\ $$$${Please}\:{tell}\:{if}\:{the}\:{answer}\:{is}\:{correct} \\ $$$${or}\:{wrong}! \\ $$
Commented by maxmathsup by imad last updated on 16/Sep/18
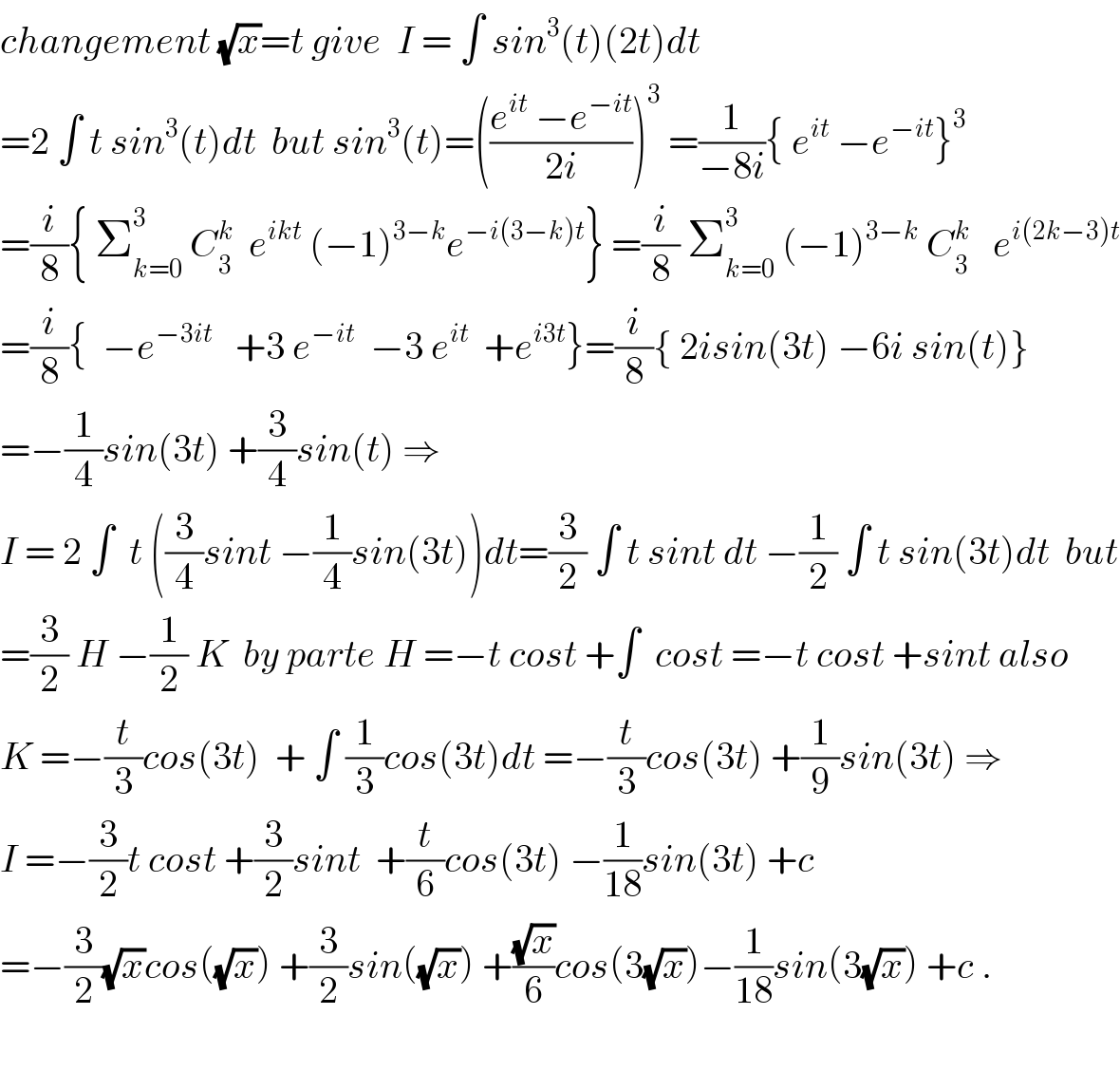
changement (√x)=t give I = ∫ sin^3 (t)(2t)dt =2 ∫ t sin^3 (t)dt but sin^3 (t)=(((e^(it) −e^(−it) )/(2i)))^3 =(1/(−8i)){ e^(it) −e^(−it) }^3 =(i/8){ Σ_(k=0) ^3 C_3 ^k e^(ikt) (−1)^(3−k) e^(−i(3−k)t) } =(i/8) Σ_(k=0) ^3 (−1)^(3−k) C_3 ^k e^(i(2k−3)t) =(i/8){ −e^(−3it) +3 e^(−it) −3 e^(it) +e^(i3t) }=(i/8){ 2isin(3t) −6i sin(t)} =−(1/4)sin(3t) +(3/4)sin(t) ⇒ I = 2 ∫ t ((3/4)sint −(1/4)sin(3t))dt=(3/2) ∫ t sint dt −(1/2) ∫ t sin(3t)dt but =(3/2) H −(1/2) K by parte H =−t cost +∫ cost =−t cost +sint also K =−(t/3)cos(3t) + ∫ (1/3)cos(3t)dt =−(t/3)cos(3t) +(1/9)sin(3t) ⇒ I =−(3/2)t cost +(3/2)sint +(t/6)cos(3t) −(1/(18))sin(3t) +c =−(3/2)(√x)cos((√x)) +(3/2)sin((√x)) +((√x)/6)cos(3(√x))−(1/(18))sin(3(√x)) +c .
$${changement}\:\sqrt{{x}}={t}\:{give}\:\:{I}\:=\:\int\:{sin}^{\mathrm{3}} \left({t}\right)\left(\mathrm{2}{t}\right){dt} \\ $$$$=\mathrm{2}\:\int\:{t}\:{sin}^{\mathrm{3}} \left({t}\right){dt}\:\:{but}\:{sin}^{\mathrm{3}} \left({t}\right)=\left(\frac{{e}^{{it}} \:−{e}^{−{it}} }{\mathrm{2}{i}}\right)^{\mathrm{3}} \:=\frac{\mathrm{1}}{−\mathrm{8}{i}}\left\{\:{e}^{{it}} \:−{e}^{−{it}} \right\}^{\mathrm{3}} \\ $$$$=\frac{{i}}{\mathrm{8}}\left\{\:\sum_{{k}=\mathrm{0}} ^{\mathrm{3}} \:{C}_{\mathrm{3}} ^{{k}} \:\:{e}^{{ikt}} \:\left(−\mathrm{1}\right)^{\mathrm{3}−{k}} {e}^{−{i}\left(\mathrm{3}−{k}\right){t}} \right\}\:=\frac{{i}}{\mathrm{8}}\:\sum_{{k}=\mathrm{0}} ^{\mathrm{3}} \:\left(−\mathrm{1}\right)^{\mathrm{3}−{k}} \:{C}_{\mathrm{3}} ^{{k}} \:\:\:{e}^{{i}\left(\mathrm{2}{k}−\mathrm{3}\right){t}} \\ $$$$=\frac{{i}}{\mathrm{8}}\left\{\:\:−{e}^{−\mathrm{3}{it}} \:\:\:+\mathrm{3}\:{e}^{−{it}} \:\:−\mathrm{3}\:{e}^{{it}} \:\:+{e}^{{i}\mathrm{3}{t}} \right\}=\frac{{i}}{\mathrm{8}}\left\{\:\mathrm{2}{isin}\left(\mathrm{3}{t}\right)\:−\mathrm{6}{i}\:{sin}\left({t}\right)\right\} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{3}{t}\right)\:+\frac{\mathrm{3}}{\mathrm{4}}{sin}\left({t}\right)\:\Rightarrow \\ $$$${I}\:=\:\mathrm{2}\:\int\:\:{t}\:\left(\frac{\mathrm{3}}{\mathrm{4}}{sint}\:−\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{3}{t}\right)\right){dt}=\frac{\mathrm{3}}{\mathrm{2}}\:\int\:{t}\:{sint}\:{dt}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int\:{t}\:{sin}\left(\mathrm{3}{t}\right){dt}\:\:{but} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\:{H}\:−\frac{\mathrm{1}}{\mathrm{2}}\:{K}\:\:{by}\:{parte}\:{H}\:=−{t}\:{cost}\:+\int\:\:{cost}\:=−{t}\:{cost}\:+{sint}\:{also} \\ $$$${K}\:=−\frac{{t}}{\mathrm{3}}{cos}\left(\mathrm{3}{t}\right)\:\:+\:\int\:\frac{\mathrm{1}}{\mathrm{3}}{cos}\left(\mathrm{3}{t}\right){dt}\:=−\frac{{t}}{\mathrm{3}}{cos}\left(\mathrm{3}{t}\right)\:+\frac{\mathrm{1}}{\mathrm{9}}{sin}\left(\mathrm{3}{t}\right)\:\Rightarrow \\ $$$${I}\:=−\frac{\mathrm{3}}{\mathrm{2}}{t}\:{cost}\:+\frac{\mathrm{3}}{\mathrm{2}}{sint}\:\:+\frac{{t}}{\mathrm{6}}{cos}\left(\mathrm{3}{t}\right)\:−\frac{\mathrm{1}}{\mathrm{18}}{sin}\left(\mathrm{3}{t}\right)\:+{c} \\ $$$$=−\frac{\mathrm{3}}{\mathrm{2}}\sqrt{{x}}{cos}\left(\sqrt{{x}}\right)\:+\frac{\mathrm{3}}{\mathrm{2}}{sin}\left(\sqrt{{x}}\right)\:+\frac{\sqrt{{x}}}{\mathrm{6}}{cos}\left(\mathrm{3}\sqrt{{x}}\right)−\frac{\mathrm{1}}{\mathrm{18}}{sin}\left(\mathrm{3}\sqrt{{x}}\right)\:+{c}\:. \\ $$$$ \\ $$
Commented by Tinkutara last updated on 16/Sep/18
Thank you very much Sir! I got the answer. ��������
Commented by maxmathsup by imad last updated on 16/Sep/18
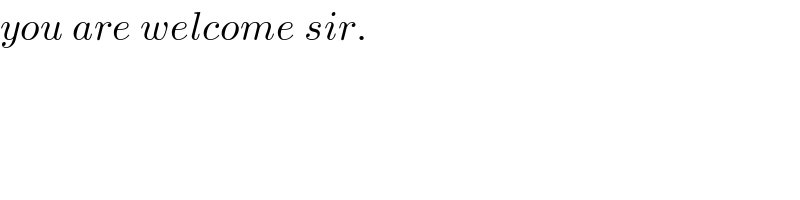
you are welcome sir.
$${you}\:{are}\:{welcome}\:{sir}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 16/Sep/18
t^2 =x ∫sin^3 t×2tdt sin3t=3sint−4sin^3 t ∫(((3sint−sin3t)/4))×2t dt (3/2)∫sint.tdt−(1/2)∫sin3t×t dt (3/2)I_1 −(1/2)I_2 ∫sint ×t dt t×−cost−∫[(dt/dt)∫sint dt]dt −tcost−∫−costdt =−tcost+sint (3/2)(−tcost+sint) (3/2)((√x) cos(√x) +sin(√x) ) ∫tsin3tdt =t×((−cos3t)/3)−∫[(dt/dt)∫sin3tdt]dt =((−tcos3t)/3)+∫((cos3t)/3) =((−tcos3t)/3)+((sin3t)/9) =((3sint−4sin^3 t)/9)+(((−t)(4cos^3 t−3cost))/3) =((3sin(√x) −4sin^3 (√x) )/9)+(((−(√x) )(4cos^3 (√x) −3cos(√x) ))/3) so (1/2)I_2 ((3sin(√x) −4sin^3 (√x))/(18))+(((−(√x) )(4cos^3 (√x) −3cos(√x) ))/6) answer is (3/2)I_1 −(1/2)I_2 (3/2)((√x) cos(√x) +sin(√x) )−{((3sin(√x) −4sin^3 (√x) )/(18))+(((−(√x) )(4cos^3 (√x) −3cos(√x) ))/6)}
$${t}^{\mathrm{2}} ={x} \\ $$$$\int{sin}^{\mathrm{3}} {t}×\mathrm{2}{tdt} \\ $$$${sin}\mathrm{3}{t}=\mathrm{3}{sint}−\mathrm{4}{sin}^{\mathrm{3}} {t} \\ $$$$\int\left(\frac{\mathrm{3}{sint}−{sin}\mathrm{3}{t}}{\mathrm{4}}\right)×\mathrm{2}{t}\:{dt} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}\int{sint}.{tdt}−\frac{\mathrm{1}}{\mathrm{2}}\int{sin}\mathrm{3}{t}×{t}\:{dt} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}{I}_{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}{I}_{\mathrm{2}} \\ $$$$\int{sint}\:×{t}\:{dt} \\ $$$${t}×−{cost}−\int\left[\frac{{dt}}{{dt}}\int{sint}\:{dt}\right]{dt} \\ $$$$−{tcost}−\int−{costdt} \\ $$$$=−{tcost}+{sint} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}\left(−{tcost}+{sint}\right) \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}\left(\sqrt{{x}}\:{cos}\sqrt{{x}}\:+{sin}\sqrt{{x}}\:\right) \\ $$$$\int{tsin}\mathrm{3}{tdt} \\ $$$$={t}×\frac{−{cos}\mathrm{3}{t}}{\mathrm{3}}−\int\left[\frac{{dt}}{{dt}}\int{sin}\mathrm{3}{tdt}\right]{dt} \\ $$$$=\frac{−{tcos}\mathrm{3}{t}}{\mathrm{3}}+\int\frac{{cos}\mathrm{3}{t}}{\mathrm{3}} \\ $$$$=\frac{−{tcos}\mathrm{3}{t}}{\mathrm{3}}+\frac{{sin}\mathrm{3}{t}}{\mathrm{9}} \\ $$$$=\frac{\mathrm{3}{sint}−\mathrm{4}{sin}^{\mathrm{3}} {t}}{\mathrm{9}}+\frac{\left(−{t}\right)\left(\mathrm{4}{cos}^{\mathrm{3}} {t}−\mathrm{3}{cost}\right)}{\mathrm{3}} \\ $$$$=\frac{\mathrm{3}{sin}\sqrt{{x}}\:−\mathrm{4}{sin}^{\mathrm{3}} \sqrt{{x}}\:}{\mathrm{9}}+\frac{\left(−\sqrt{{x}}\:\right)\left(\mathrm{4}{cos}^{\mathrm{3}} \sqrt{{x}}\:−\mathrm{3}{cos}\sqrt{{x}}\:\right)}{\mathrm{3}} \\ $$$${so} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{I}_{\mathrm{2}} \\ $$$$\frac{\mathrm{3}{sin}\sqrt{{x}}\:−\mathrm{4}{sin}^{\mathrm{3}} \sqrt{{x}}}{\mathrm{18}}+\frac{\left(−\sqrt{{x}}\:\right)\left(\mathrm{4}{cos}^{\mathrm{3}} \sqrt{{x}}\:−\mathrm{3}{cos}\sqrt{{x}}\:\right)}{\mathrm{6}} \\ $$$${answer}\:{is}\:\frac{\mathrm{3}}{\mathrm{2}}{I}_{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}{I}_{\mathrm{2}} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}\left(\sqrt{{x}}\:{cos}\sqrt{{x}}\:+{sin}\sqrt{{x}}\:\right)−\left\{\frac{\mathrm{3}{sin}\sqrt{{x}}\:−\mathrm{4}{sin}^{\mathrm{3}} \sqrt{{x}}\:}{\mathrm{18}}+\frac{\left(−\sqrt{{x}}\:\right)\left(\mathrm{4}{cos}^{\mathrm{3}} \sqrt{{x}}\:−\mathrm{3}{cos}\sqrt{{x}}\:\right)}{\mathrm{6}}\right\} \\ $$$$ \\ $$$$ \\ $$
Commented by Tinkutara last updated on 16/Sep/18
Thank you very much Sir! I got the answer. ��������

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *