Question Number 97322 by student work last updated on 07/Jun/20

$$\int\mathrm{sin}\:^{\mathrm{4}} \mathrm{x}\centerdot\mathrm{cos}\:^{\mathrm{5}} \mathrm{xdx}=? \\ $$
Answered by bemath last updated on 08/Jun/20
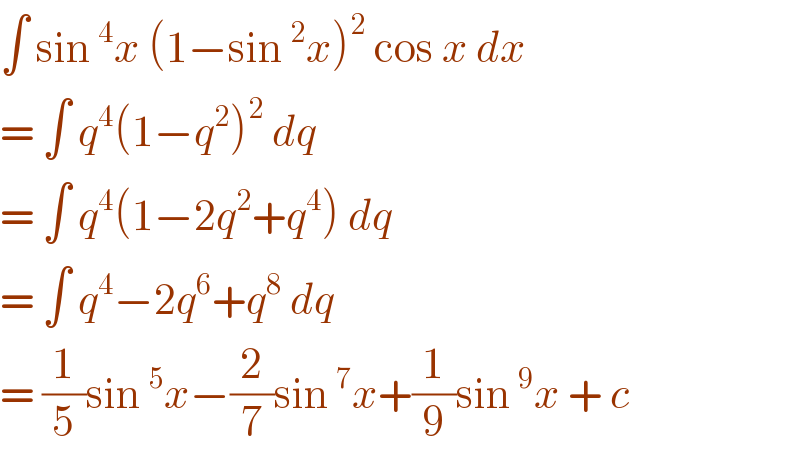
$$\int\:\mathrm{sin}\:^{\mathrm{4}} {x}\:\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {x}\right)^{\mathrm{2}} \:\mathrm{cos}\:{x}\:{dx} \\ $$$$=\:\int\:{q}^{\mathrm{4}} \left(\mathrm{1}−{q}^{\mathrm{2}} \right)^{\mathrm{2}} \:{dq}\: \\ $$$$=\:\int\:{q}^{\mathrm{4}} \left(\mathrm{1}−\mathrm{2}{q}^{\mathrm{2}} +{q}^{\mathrm{4}} \right)\:{dq} \\ $$$$=\:\int\:{q}^{\mathrm{4}} −\mathrm{2}{q}^{\mathrm{6}} +{q}^{\mathrm{8}} \:{dq} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{5}}\mathrm{sin}\:^{\mathrm{5}} {x}−\frac{\mathrm{2}}{\mathrm{7}}\mathrm{sin}\:^{\mathrm{7}} {x}+\frac{\mathrm{1}}{\mathrm{9}}\mathrm{sin}\:^{\mathrm{9}} {x}\:+\:{c} \\ $$
Commented by Aziztisffola last updated on 07/Jun/20

$$\frac{\mathrm{2}}{\mathrm{7}}\mathrm{sin}^{\mathrm{7}} \left(\mathrm{x}\right) \\ $$
Commented by Rohit@Thakur last updated on 07/Jun/20

$$\frac{\mathrm{2}}{\mathrm{7}}{sin}^{\mathrm{7}} \left({x}\right) \\ $$
Commented by bemath last updated on 08/Jun/20

$$\mathrm{yes}.\:\mathrm{typo} \\ $$
