Menu Close

sin-4-x-dx-4-cos-2-x-

Tinku Tara 0 Comments
Pin




Question Number 89584 by jagoll last updated on 18/Apr/20
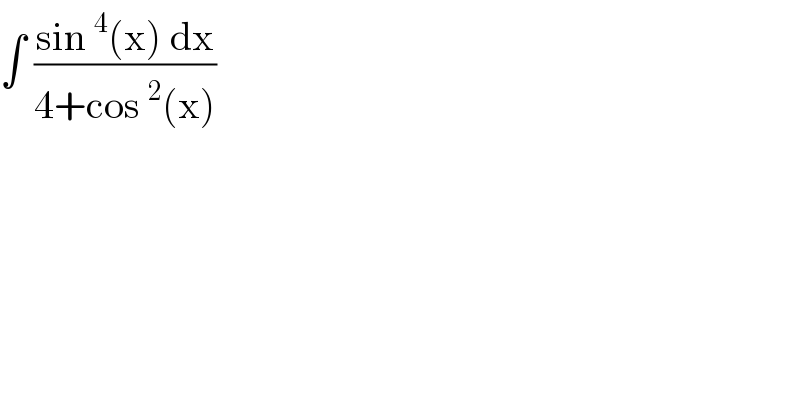
∫ ((sin^4 (x) dx)/(4+cos^2 (x)))
$$\int\:\frac{\mathrm{sin}\:^{\mathrm{4}} \left(\mathrm{x}\right)\:\mathrm{dx}}{\mathrm{4}+\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{x}\right)} \\ $$
Commented by mathmax by abdo last updated on 18/Apr/20
I =∫ ((sin^4 xdx)/(4+cos^2 x)) =∫ (((((1−cos(2x))/2))^2 )/(4+((1−cos(2x))/2)))dx =(1/2) ∫ ((1−2cos(2x)+cos^2 (2x))/(9−cos(2x)))dx ((u^2 −2u+1)/(9−u)) =−((u^2 −81 −2u +82)/(u−9)) =−(u+9)+((2u−82)/(u−9)) ⇒ I =−(1/2)∫(cos(2x)+9)dx +∫((cos(2x)−41)/(cos(2x)−9))dx [we have ∫(cos(2x)+9)dx =9x +(1/2)sin(2x) +c_1 ∫ ((cos(2x)−41)/(cos(2x)−9)) =_(2x=t) (1/2)∫ ((cost−41)/(cost−9))dt =(1/2)∫ ((cost−9 +9−41)/(cost−9))dt =(t/2)−16 ∫ (dt/(cost−9)) and ∫ (dt/(cost−9)) =_(tan((t/2))=z) ∫ ((2dz)/((1+z^2 )(((1−z^2 )/(1+z^2 ))−9))) =2∫ (dz/(1−z^2 −9−z^2 )) =2∫ (dz/(−8−2z^2 )) =−∫ (dz/(4+z^2 )) =_(z=2α) −∫ ((2dα)/(4(1+α^(2)) )) =−(1/2)arctan(α)+c_2 =−(1/2)arctan((1/2)tan(x)) +c_2 ⇒ I =−(9/2)x−(1/4)sin(2x) +x−16(−(1/2) arctan(((tanx)/2))+c_2 ) I =−(7/2)x −(1/4)sin(2x) +8 arctan(((tanx)/2))+C
$${I}\:=\int\:\:\frac{{sin}^{\mathrm{4}} {xdx}}{\mathrm{4}+{cos}^{\mathrm{2}} {x}}\:=\int\:\frac{\left(\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{4}+\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\frac{\mathrm{1}−\mathrm{2}{cos}\left(\mathrm{2}{x}\right)+{cos}^{\mathrm{2}} \left(\mathrm{2}{x}\right)}{\mathrm{9}−{cos}\left(\mathrm{2}{x}\right)}{dx} \\ $$$$\frac{{u}^{\mathrm{2}} −\mathrm{2}{u}+\mathrm{1}}{\mathrm{9}−{u}}\:=−\frac{{u}^{\mathrm{2}} −\mathrm{81}\:−\mathrm{2}{u}\:+\mathrm{82}}{{u}−\mathrm{9}}\:=−\left({u}+\mathrm{9}\right)+\frac{\mathrm{2}{u}−\mathrm{82}}{{u}−\mathrm{9}}\:\Rightarrow \\ $$$${I}\:=−\frac{\mathrm{1}}{\mathrm{2}}\int\left({cos}\left(\mathrm{2}{x}\right)+\mathrm{9}\right){dx}\:+\int\frac{{cos}\left(\mathrm{2}{x}\right)−\mathrm{41}}{{cos}\left(\mathrm{2}{x}\right)−\mathrm{9}}{dx}\:\left[{we}\:{have}\right. \\ $$$$\int\left({cos}\left(\mathrm{2}{x}\right)+\mathrm{9}\right){dx}\:=\mathrm{9}{x}\:+\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}{x}\right)\:+{c}_{\mathrm{1}} \\ $$$$\int\:\frac{{cos}\left(\mathrm{2}{x}\right)−\mathrm{41}}{{cos}\left(\mathrm{2}{x}\right)−\mathrm{9}}\:=_{\mathrm{2}{x}={t}} \:\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{cost}−\mathrm{41}}{{cost}−\mathrm{9}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{cost}−\mathrm{9}\:+\mathrm{9}−\mathrm{41}}{{cost}−\mathrm{9}}{dt}\:=\frac{{t}}{\mathrm{2}}−\mathrm{16}\:\int\:\:\frac{{dt}}{{cost}−\mathrm{9}}\:{and} \\ $$$$\int\:\:\frac{{dt}}{{cost}−\mathrm{9}}\:=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={z}} \:\:\:\int\:\:\frac{\mathrm{2}{dz}}{\left(\mathrm{1}+{z}^{\mathrm{2}} \right)\left(\frac{\mathrm{1}−{z}^{\mathrm{2}} }{\mathrm{1}+{z}^{\mathrm{2}} }−\mathrm{9}\right)} \\ $$$$=\mathrm{2}\int\:\:\frac{{dz}}{\mathrm{1}−{z}^{\mathrm{2}} −\mathrm{9}−{z}^{\mathrm{2}} }\:=\mathrm{2}\int\:\:\:\frac{{dz}}{−\mathrm{8}−\mathrm{2}{z}^{\mathrm{2}} }\:=−\int\:\:\frac{{dz}}{\mathrm{4}+{z}^{\mathrm{2}} } \\ $$$$=_{{z}=\mathrm{2}\alpha} \:\:−\int\:\frac{\mathrm{2}{d}\alpha}{\mathrm{4}\left(\mathrm{1}+\alpha^{\left.\mathrm{2}\right)} \right.}\:=−\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\alpha\right)+{c}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}}{arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}{tan}\left({x}\right)\right)\:+{c}_{\mathrm{2}} \\ $$$$\Rightarrow\:{I}\:=−\frac{\mathrm{9}}{\mathrm{2}}{x}−\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{2}{x}\right)\:+{x}−\mathrm{16}\left(−\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}\left(\frac{{tanx}}{\mathrm{2}}\right)+{c}_{\mathrm{2}} \right) \\ $$$${I}\:=−\frac{\mathrm{7}}{\mathrm{2}}{x}\:−\frac{\mathrm{1}}{\mathrm{4}}{sin}\left(\mathrm{2}{x}\right)\:+\mathrm{8}\:{arctan}\left(\frac{{tanx}}{\mathrm{2}}\right)+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *