Question Number 20450 by tammi last updated on 27/Aug/17

$$\int\mathrm{sin}\:^{\mathrm{4}} {x}\mathrm{cos}\:^{\mathrm{3}} {xdx} \\ $$
Answered by mrW1 last updated on 27/Aug/17
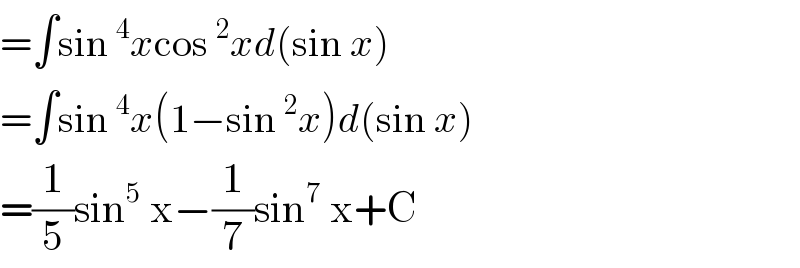
$$=\int\mathrm{sin}\:^{\mathrm{4}} {x}\mathrm{cos}\:^{\mathrm{2}} {xd}\left(\mathrm{sin}\:{x}\right) \\ $$$$=\int\mathrm{sin}\:^{\mathrm{4}} {x}\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {x}\right){d}\left(\mathrm{sin}\:{x}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{sin}^{\mathrm{5}} \:\mathrm{x}−\frac{\mathrm{1}}{\mathrm{7}}\mathrm{sin}^{\mathrm{7}} \:\mathrm{x}+\mathrm{C} \\ $$
