Question Number 20389 by tammi last updated on 26/Aug/17

$$\int\mathrm{sin}\:^{\mathrm{4}} {xdx} \\ $$
Answered by Joel577 last updated on 26/Aug/17
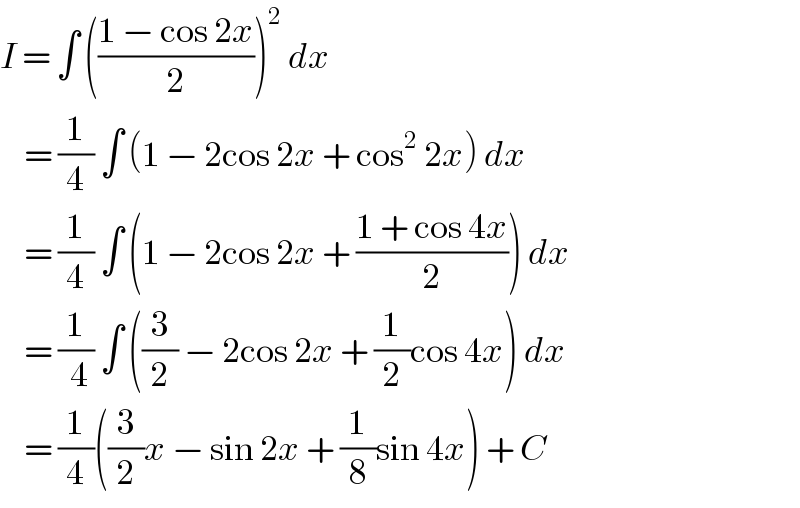
$${I}\:=\:\int\:\left(\frac{\mathrm{1}\:−\:\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}}\right)^{\mathrm{2}} \:{dx} \\ $$$$\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:\int\:\left(\mathrm{1}\:−\:\mathrm{2cos}\:\mathrm{2}{x}\:+\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}{x}\right)\:{dx} \\ $$$$\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:\int\:\left(\mathrm{1}\:−\:\mathrm{2cos}\:\mathrm{2}{x}\:+\:\frac{\mathrm{1}\:+\:\mathrm{cos}\:\mathrm{4}{x}}{\mathrm{2}}\right)\:{dx} \\ $$$$\:\:\:\:=\:\frac{\mathrm{1}}{\:\mathrm{4}}\:\int\:\left(\frac{\mathrm{3}}{\mathrm{2}}\:−\:\mathrm{2cos}\:\mathrm{2}{x}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{4}{x}\right)\:{dx} \\ $$$$\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{3}}{\mathrm{2}}{x}\:−\:\mathrm{sin}\:\mathrm{2}{x}\:+\:\frac{\mathrm{1}}{\mathrm{8}}\mathrm{sin}\:\mathrm{4}{x}\right)\:+\:{C} \\ $$
