Menu Close

sin-4sin-1-x-sin-2sin-1-x-

Tinku Tara 0 Comments
Pin




Question Number 116768 by bemath last updated on 06/Oct/20
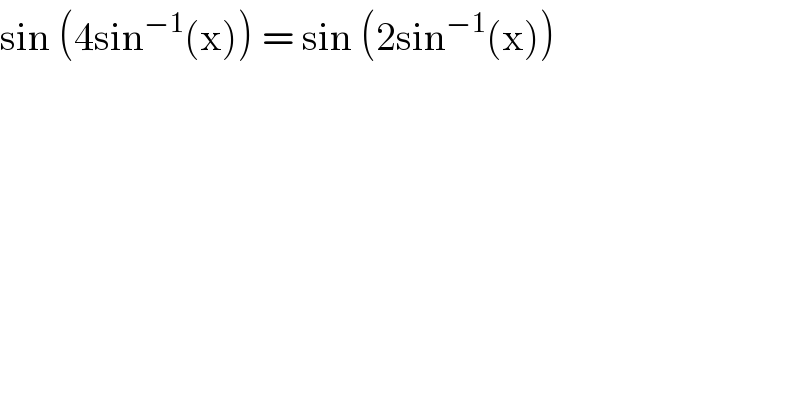
sin (4sin^(−1) (x)) = sin (2sin^(−1) (x))
$$\mathrm{sin}\:\left(\mathrm{4sin}^{−\mathrm{1}} \left(\mathrm{x}\right)\right)\:=\:\mathrm{sin}\:\left(\mathrm{2sin}^{−\mathrm{1}} \left(\mathrm{x}\right)\right) \\ $$
Answered by bobhans last updated on 06/Oct/20
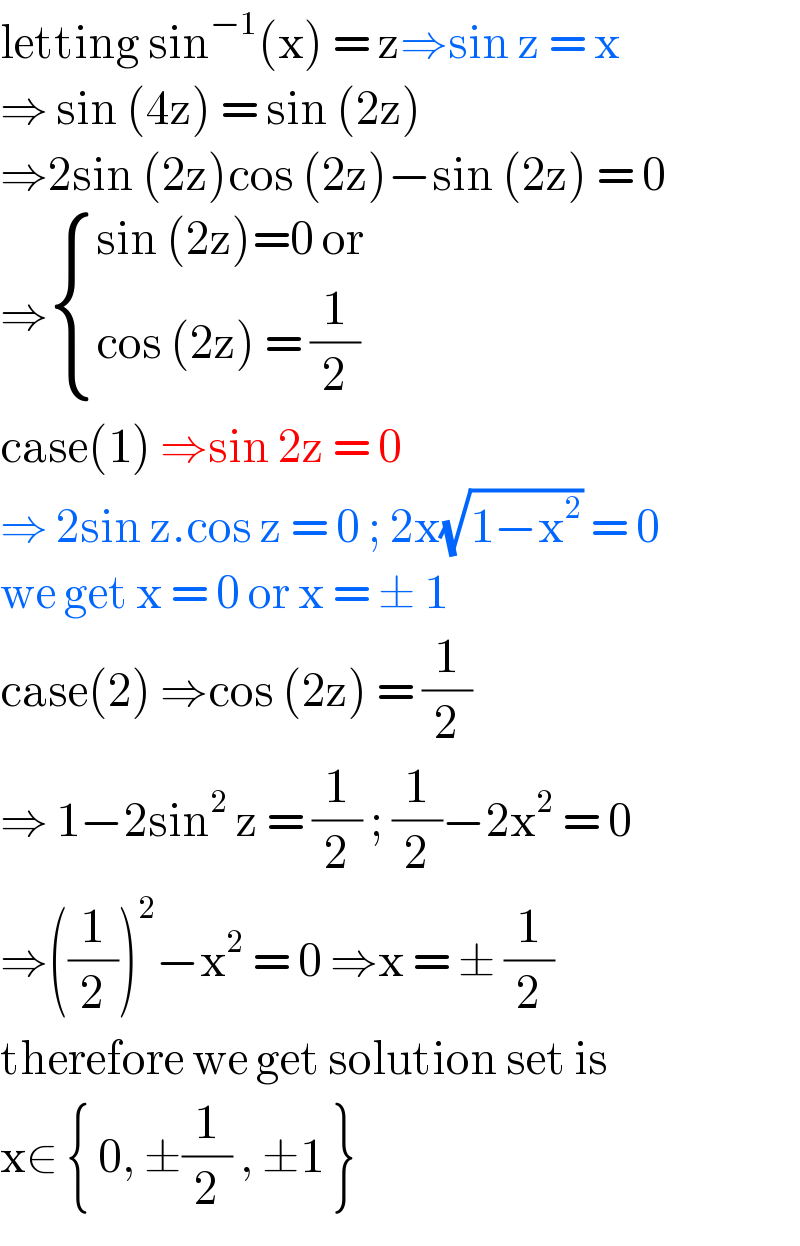
letting sin^(−1) (x) = z⇒sin z = x ⇒ sin (4z) = sin (2z) ⇒2sin (2z)cos (2z)−sin (2z) = 0 ⇒ { ((sin (2z)=0 or)),((cos (2z) = (1/2))) :} case(1) ⇒sin 2z = 0 ⇒ 2sin z.cos z = 0 ; 2x(√(1−x^2 )) = 0 we get x = 0 or x = ± 1 case(2) ⇒cos (2z) = (1/2) ⇒ 1−2sin^2 z = (1/2) ; (1/2)−2x^2 = 0 ⇒((1/2))^2 −x^2 = 0 ⇒x = ± (1/2) therefore we get solution set is x∈ { 0, ±(1/2) , ±1 }
$$\mathrm{letting}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{x}\right)\:=\:\mathrm{z}\Rightarrow\mathrm{sin}\:\mathrm{z}\:=\:\mathrm{x} \\ $$$$\Rightarrow\:\mathrm{sin}\:\left(\mathrm{4z}\right)\:=\:\mathrm{sin}\:\left(\mathrm{2z}\right)\: \\ $$$$\Rightarrow\mathrm{2sin}\:\left(\mathrm{2z}\right)\mathrm{cos}\:\left(\mathrm{2z}\right)−\mathrm{sin}\:\left(\mathrm{2z}\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\begin{cases}{\mathrm{sin}\:\left(\mathrm{2z}\right)=\mathrm{0}\:\mathrm{or}}\\{\mathrm{cos}\:\left(\mathrm{2z}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}}\end{cases} \\ $$$$\mathrm{case}\left(\mathrm{1}\right)\:\Rightarrow\mathrm{sin}\:\mathrm{2z}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{2sin}\:\mathrm{z}.\mathrm{cos}\:\mathrm{z}\:=\:\mathrm{0}\:;\:\mathrm{2x}\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:=\:\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{x}\:=\:\mathrm{0}\:\mathrm{or}\:\mathrm{x}\:=\:\pm\:\mathrm{1} \\ $$$$\mathrm{case}\left(\mathrm{2}\right)\:\Rightarrow\mathrm{cos}\:\left(\mathrm{2z}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \:\mathrm{z}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:;\:\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2x}^{\mathrm{2}} \:=\:\mathrm{0}\: \\ $$$$\Rightarrow\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} \:=\:\mathrm{0}\:\Rightarrow\mathrm{x}\:=\:\pm\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{therefore}\:\mathrm{we}\:\mathrm{get}\:\mathrm{solution}\:\mathrm{set}\:\mathrm{is}\: \\ $$$$\mathrm{x}\in\:\left\{\:\mathrm{0},\:\pm\frac{\mathrm{1}}{\mathrm{2}}\:,\:\pm\mathrm{1}\:\right\} \\ $$
Answered by MJS_new last updated on 06/Oct/20
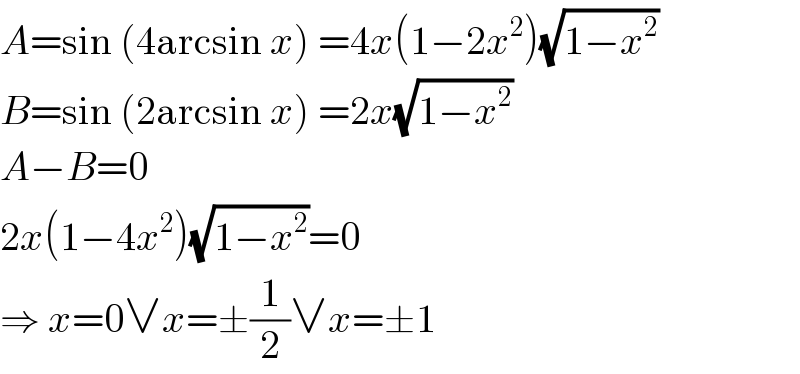
A=sin (4arcsin x) =4x(1−2x^2 )(√(1−x^2 )) B=sin (2arcsin x) =2x(√(1−x^2 )) A−B=0 2x(1−4x^2 )(√(1−x^2 ))=0 ⇒ x=0∨x=±(1/2)∨x=±1
$${A}=\mathrm{sin}\:\left(\mathrm{4arcsin}\:{x}\right)\:=\mathrm{4}{x}\left(\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${B}=\mathrm{sin}\:\left(\mathrm{2arcsin}\:{x}\right)\:=\mathrm{2}{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${A}−{B}=\mathrm{0} \\ $$$$\mathrm{2}{x}\left(\mathrm{1}−\mathrm{4}{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow\:{x}=\mathrm{0}\vee{x}=\pm\frac{\mathrm{1}}{\mathrm{2}}\vee{x}=\pm\mathrm{1} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *