Question Number 163822 by mkam last updated on 11/Jan/22
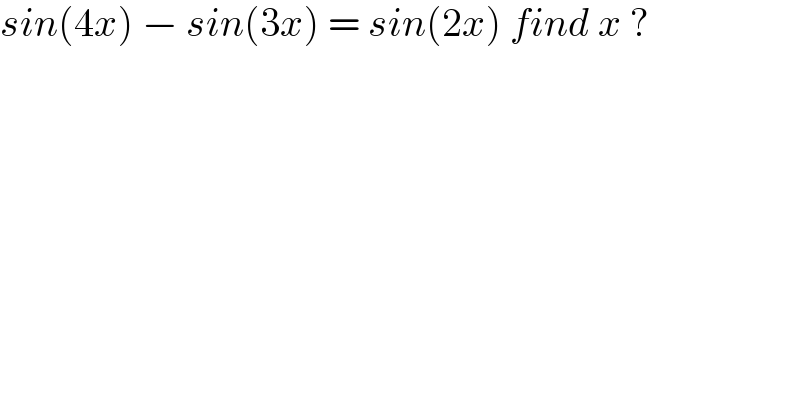
$${sin}\left(\mathrm{4}{x}\right)\:−\:{sin}\left(\mathrm{3}{x}\right)\:=\:{sin}\left(\mathrm{2}{x}\right)\:{find}\:{x}\:? \\ $$
Answered by cortano1 last updated on 11/Jan/22

Commented by mr W last updated on 11/Jan/22

$${please}\:{recheck}.\:{i}\:{think}\:{answer}\:{is} \\ $$$${wrong}. \\ $$
Commented by cortano1 last updated on 11/Jan/22

$${what}\:{wrong}\:! \\ $$
Commented by mr W last updated on 11/Jan/22

$${x}=\pm\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{2}−\sqrt[{\mathrm{3}}]{\mathrm{10}}−\sqrt[{\mathrm{3}}]{\mathrm{100}}}{\mathrm{6}}+\mathrm{2}{k}\pi\:{doesn}'{t} \\ $$$${fulfill}\:{the}\:{equation}. \\ $$
Answered by mr W last updated on 11/Jan/22
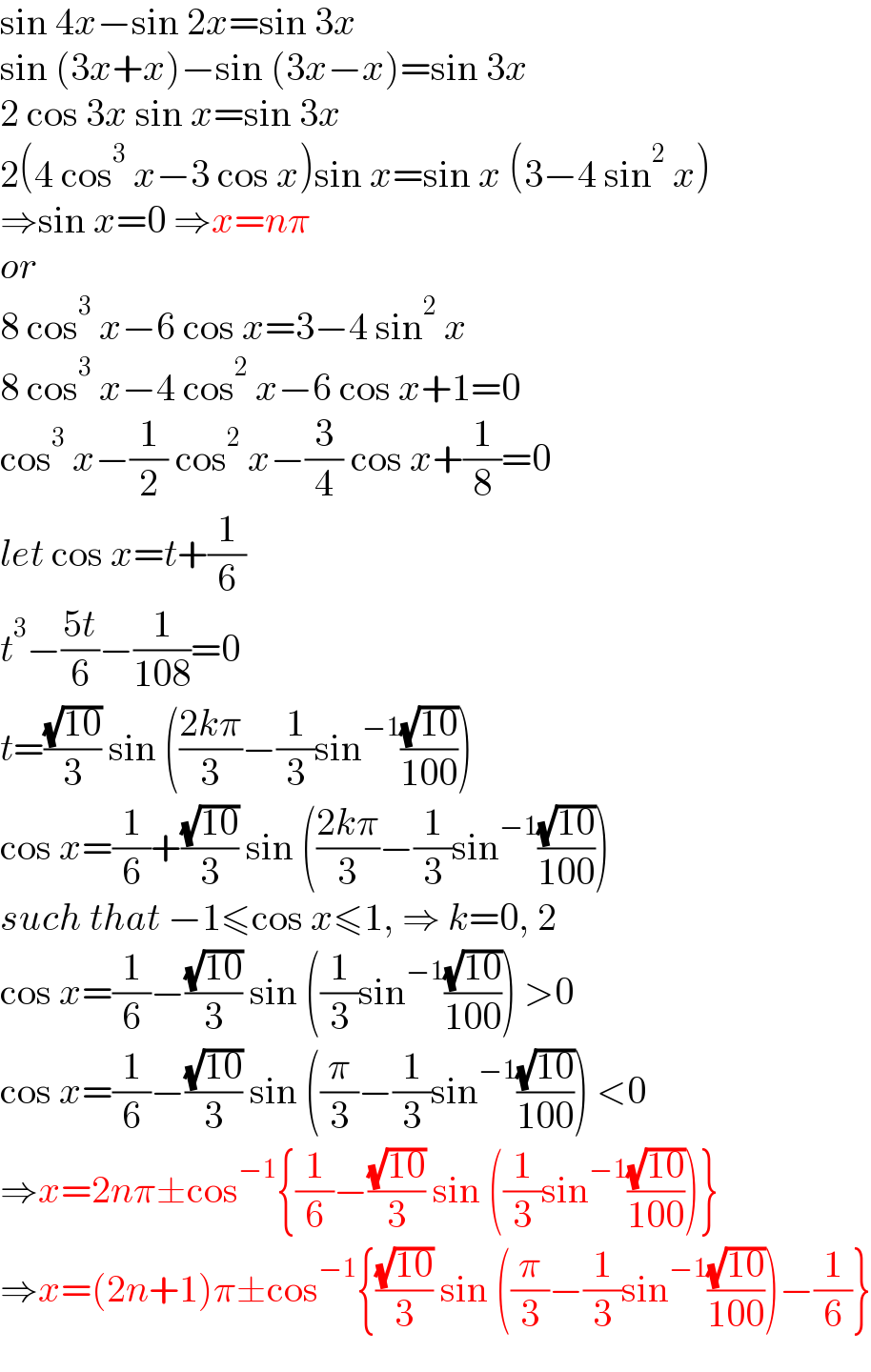
$$\mathrm{sin}\:\mathrm{4}{x}−\mathrm{sin}\:\mathrm{2}{x}=\mathrm{sin}\:\mathrm{3}{x} \\ $$$$\mathrm{sin}\:\left(\mathrm{3}{x}+{x}\right)−\mathrm{sin}\:\left(\mathrm{3}{x}−{x}\right)=\mathrm{sin}\:\mathrm{3}{x} \\ $$$$\mathrm{2}\:\mathrm{cos}\:\mathrm{3}{x}\:\mathrm{sin}\:{x}=\mathrm{sin}\:\mathrm{3}{x} \\ $$$$\mathrm{2}\left(\mathrm{4}\:\mathrm{cos}^{\mathrm{3}} \:{x}−\mathrm{3}\:\mathrm{cos}\:{x}\right)\mathrm{sin}\:{x}=\mathrm{sin}\:{x}\:\left(\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:{x}\right) \\ $$$$\Rightarrow\mathrm{sin}\:{x}=\mathrm{0}\:\Rightarrow{x}={n}\pi \\ $$$${or} \\ $$$$\mathrm{8}\:\mathrm{cos}^{\mathrm{3}} \:{x}−\mathrm{6}\:\mathrm{cos}\:{x}=\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:{x} \\ $$$$\mathrm{8}\:\mathrm{cos}^{\mathrm{3}} \:{x}−\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:{x}−\mathrm{6}\:\mathrm{cos}\:{x}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{cos}^{\mathrm{3}} \:{x}−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{cos}^{\mathrm{2}} \:{x}−\frac{\mathrm{3}}{\mathrm{4}}\:\mathrm{cos}\:{x}+\frac{\mathrm{1}}{\mathrm{8}}=\mathrm{0} \\ $$$${let}\:\mathrm{cos}\:{x}={t}+\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${t}^{\mathrm{3}} −\frac{\mathrm{5}{t}}{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{108}}=\mathrm{0} \\ $$$${t}=\frac{\sqrt{\mathrm{10}}}{\mathrm{3}}\:\mathrm{sin}\:\left(\frac{\mathrm{2}{k}\pi}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{10}}}{\mathrm{100}}\right) \\ $$$$\mathrm{cos}\:{x}=\frac{\mathrm{1}}{\mathrm{6}}+\frac{\sqrt{\mathrm{10}}}{\mathrm{3}}\:\mathrm{sin}\:\left(\frac{\mathrm{2}{k}\pi}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{10}}}{\mathrm{100}}\right) \\ $$$${such}\:{that}\:−\mathrm{1}\leqslant\mathrm{cos}\:{x}\leqslant\mathrm{1},\:\Rightarrow\:{k}=\mathrm{0},\:\mathrm{2} \\ $$$$\mathrm{cos}\:{x}=\frac{\mathrm{1}}{\mathrm{6}}−\frac{\sqrt{\mathrm{10}}}{\mathrm{3}}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{10}}}{\mathrm{100}}\right)\:>\mathrm{0} \\ $$$$\mathrm{cos}\:{x}=\frac{\mathrm{1}}{\mathrm{6}}−\frac{\sqrt{\mathrm{10}}}{\mathrm{3}}\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{10}}}{\mathrm{100}}\right)\:<\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{2}{n}\pi\pm\mathrm{cos}^{−\mathrm{1}} \left\{\frac{\mathrm{1}}{\mathrm{6}}−\frac{\sqrt{\mathrm{10}}}{\mathrm{3}}\:\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{10}}}{\mathrm{100}}\right)\right\} \\ $$$$\Rightarrow{x}=\left(\mathrm{2}{n}+\mathrm{1}\right)\pi\pm\mathrm{cos}^{−\mathrm{1}} \left\{\frac{\sqrt{\mathrm{10}}}{\mathrm{3}}\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{10}}}{\mathrm{100}}\right)−\frac{\mathrm{1}}{\mathrm{6}}\right\} \\ $$
Commented by peter frank last updated on 11/Jan/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
