Question Number 21720 by Isse last updated on 01/Oct/17

$$\int{sin}^{\mathrm{5}} \theta{d}\theta \\ $$
Answered by sma3l2996 last updated on 02/Oct/17
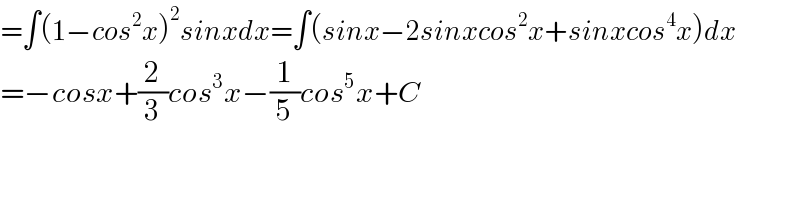
$$=\int\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right)^{\mathrm{2}} {sinxdx}=\int\left({sinx}−\mathrm{2}{sinxcos}^{\mathrm{2}} {x}+{sinxcos}^{\mathrm{4}} {x}\right){dx} \\ $$$$=−{cosx}+\frac{\mathrm{2}}{\mathrm{3}}{cos}^{\mathrm{3}} {x}−\frac{\mathrm{1}}{\mathrm{5}}{cos}^{\mathrm{5}} {x}+{C} \\ $$
