Question Number 97759 by bobhans last updated on 09/Jun/20
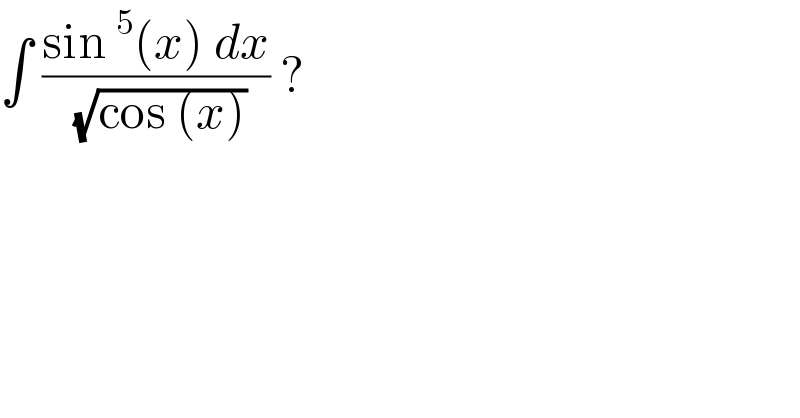
$$\int\:\frac{\mathrm{sin}\:^{\mathrm{5}} \left({x}\right)\:{dx}}{\:\sqrt{\mathrm{cos}\:\left({x}\right)}}\:? \\ $$
Answered by bemath last updated on 09/Jun/20
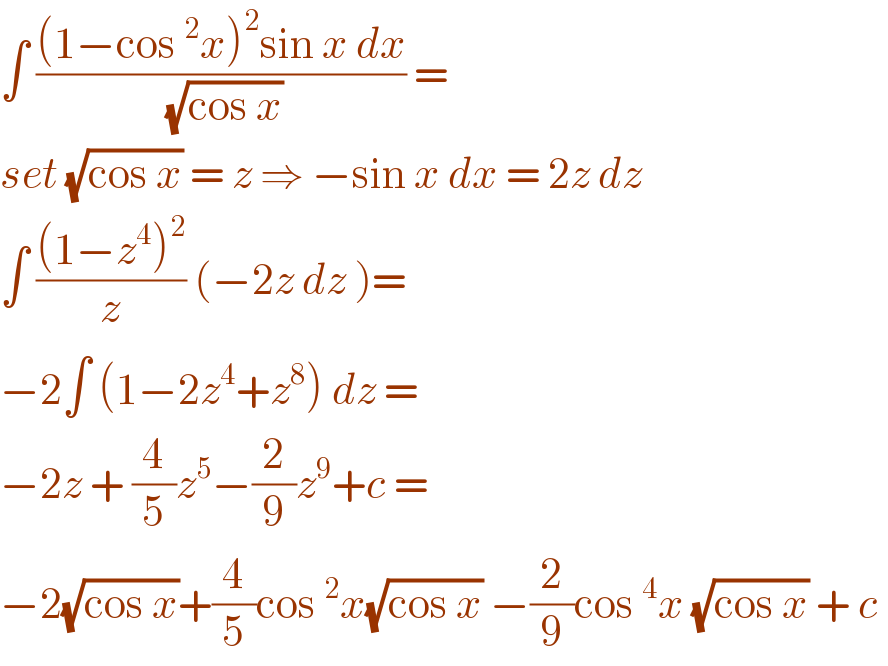
$$\int\:\frac{\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {x}\right)^{\mathrm{2}} \mathrm{sin}\:{x}\:{dx}}{\:\sqrt{\mathrm{cos}\:{x}}}\:= \\ $$$${set}\:\sqrt{\mathrm{cos}\:{x}}\:=\:{z}\:\Rightarrow\:−\mathrm{sin}\:{x}\:{dx}\:=\:\mathrm{2}{z}\:{dz} \\ $$$$\int\:\frac{\left(\mathrm{1}−{z}^{\mathrm{4}} \right)^{\mathrm{2}} }{{z}}\:\left(−\mathrm{2}{z}\:{dz}\:\right)= \\ $$$$−\mathrm{2}\int\:\left(\mathrm{1}−\mathrm{2}{z}^{\mathrm{4}} +{z}^{\mathrm{8}} \right)\:{dz}\:= \\ $$$$−\mathrm{2}{z}\:+\:\frac{\mathrm{4}}{\mathrm{5}}{z}^{\mathrm{5}} −\frac{\mathrm{2}}{\mathrm{9}}{z}^{\mathrm{9}} +{c}\:= \\ $$$$−\mathrm{2}\sqrt{\mathrm{cos}\:{x}}+\frac{\mathrm{4}}{\mathrm{5}}\mathrm{cos}\:^{\mathrm{2}} {x}\sqrt{\mathrm{cos}\:{x}}\:−\frac{\mathrm{2}}{\mathrm{9}}\mathrm{cos}\:^{\mathrm{4}} {x}\:\sqrt{\mathrm{cos}\:{x}}\:+\:{c}\: \\ $$
Commented by bobhans last updated on 09/Jun/20

$$\mathrm{alright} \\ $$
