Menu Close

sin-6-2x-dx-

Tinku Tara 0 Comments
Pin




Question Number 118218 by bemath last updated on 16/Oct/20
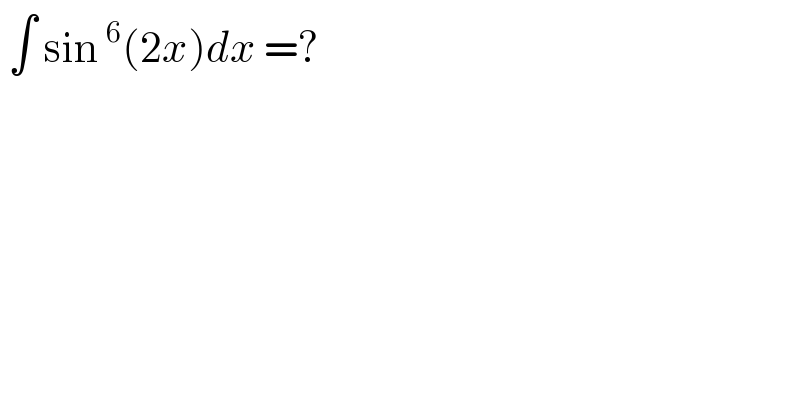
∫ sin^6 (2x)dx =?
$$\:\int\:\mathrm{sin}\:^{\mathrm{6}} \left(\mathrm{2}{x}\right){dx}\:=?\: \\ $$
Answered by bobhans last updated on 16/Oct/20
Solve ∫ sin^6 (2x) dx . by De′moivre theorem letting z = cos 2x+i sin 2x and (1/z)=cos 2x−i sin 2x ⇒and z^n = cos 2nx+i sin 2nx ; (1/z^n )=cos 2nx−i sin 2nx; in generally ⇒z^n +(1/z^n )= 2cos 2nx ; z^6 +(1/z^6 ) = 2cos 12x we get ⇒2i sin 2x = z−(1/z) then (2i sin 2x)^6 = (z−(1/z))^6 ⇒−64 sin^6 2x = (z^6 +(1/z^6 ))−6(z^4 +(1/z^4 ))+15(z^2 +(1/z^2 ))−20 gives ∫sin^6 2x dx = −(1/(64))∫(2cos 12x−6(2cos 8x)+15(2cos 4x)−20)dx =−(1/(32))∫cos 12x−6cos 8x+15cos 4x−10)dx = −(1/(32)) [ ((sin 12x)/(12)) −((3sin 8x)/4) +((15sin 4x)/4) −10x ] + c
$$\:\mathrm{Solve}\:\int\:\mathrm{sin}\:^{\mathrm{6}} \left(\mathrm{2x}\right)\:\mathrm{dx}\:. \\ $$$$\mathrm{by}\:\mathrm{De}'\mathrm{moivre}\:\mathrm{theorem}\: \\ $$$$\mathrm{letting}\:\mathrm{z}\:=\:\mathrm{cos}\:\mathrm{2x}+\mathrm{i}\:\mathrm{sin}\:\mathrm{2x}\:\mathrm{and}\:\frac{\mathrm{1}}{\mathrm{z}}=\mathrm{cos}\:\mathrm{2x}−\mathrm{i}\:\mathrm{sin}\:\mathrm{2x} \\ $$$$\Rightarrow\mathrm{and}\:\mathrm{z}^{\mathrm{n}} \:=\:\mathrm{cos}\:\mathrm{2nx}+\mathrm{i}\:\mathrm{sin}\:\mathrm{2nx}\:;\:\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{n}} }=\mathrm{cos}\:\mathrm{2nx}−\mathrm{i}\:\mathrm{sin}\:\mathrm{2nx};\:\mathrm{in}\:\mathrm{generally} \\ $$$$\Rightarrow\mathrm{z}^{\mathrm{n}} +\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{n}} }=\:\mathrm{2cos}\:\mathrm{2nx}\:;\:\mathrm{z}^{\mathrm{6}} +\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{6}} }\:=\:\mathrm{2cos}\:\mathrm{12x} \\ $$$$\mathrm{we}\:\mathrm{get}\:\Rightarrow\mathrm{2i}\:\mathrm{sin}\:\mathrm{2x}\:=\:\mathrm{z}−\frac{\mathrm{1}}{\mathrm{z}} \\ $$$$\mathrm{then}\:\left(\mathrm{2i}\:\mathrm{sin}\:\mathrm{2x}\right)^{\mathrm{6}} \:=\:\left(\mathrm{z}−\frac{\mathrm{1}}{\mathrm{z}}\right)^{\mathrm{6}} \\ $$$$\Rightarrow−\mathrm{64}\:\mathrm{sin}\:^{\mathrm{6}} \mathrm{2x}\:=\:\left(\mathrm{z}^{\mathrm{6}} +\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{6}} }\right)−\mathrm{6}\left(\mathrm{z}^{\mathrm{4}} +\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{4}} }\right)+\mathrm{15}\left(\mathrm{z}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} }\right)−\mathrm{20} \\ $$$$\mathrm{gives}\:\int\mathrm{sin}\:^{\mathrm{6}} \mathrm{2x}\:\mathrm{dx}\:=\:−\frac{\mathrm{1}}{\mathrm{64}}\int\left(\mathrm{2cos}\:\mathrm{12x}−\mathrm{6}\left(\mathrm{2cos}\:\mathrm{8x}\right)+\mathrm{15}\left(\mathrm{2cos}\:\mathrm{4x}\right)−\mathrm{20}\right)\mathrm{dx} \\ $$$$\left.=−\frac{\mathrm{1}}{\mathrm{32}}\int\mathrm{cos}\:\mathrm{12x}−\mathrm{6cos}\:\mathrm{8x}+\mathrm{15cos}\:\mathrm{4x}−\mathrm{10}\right)\mathrm{dx} \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{32}}\:\left[\:\frac{\mathrm{sin}\:\mathrm{12x}}{\mathrm{12}}\:−\frac{\mathrm{3sin}\:\mathrm{8x}}{\mathrm{4}}\:+\frac{\mathrm{15sin}\:\mathrm{4x}}{\mathrm{4}}\:−\mathrm{10x}\:\right]\:+\:\mathrm{c} \\ $$
Answered by 1549442205PVT last updated on 16/Oct/20
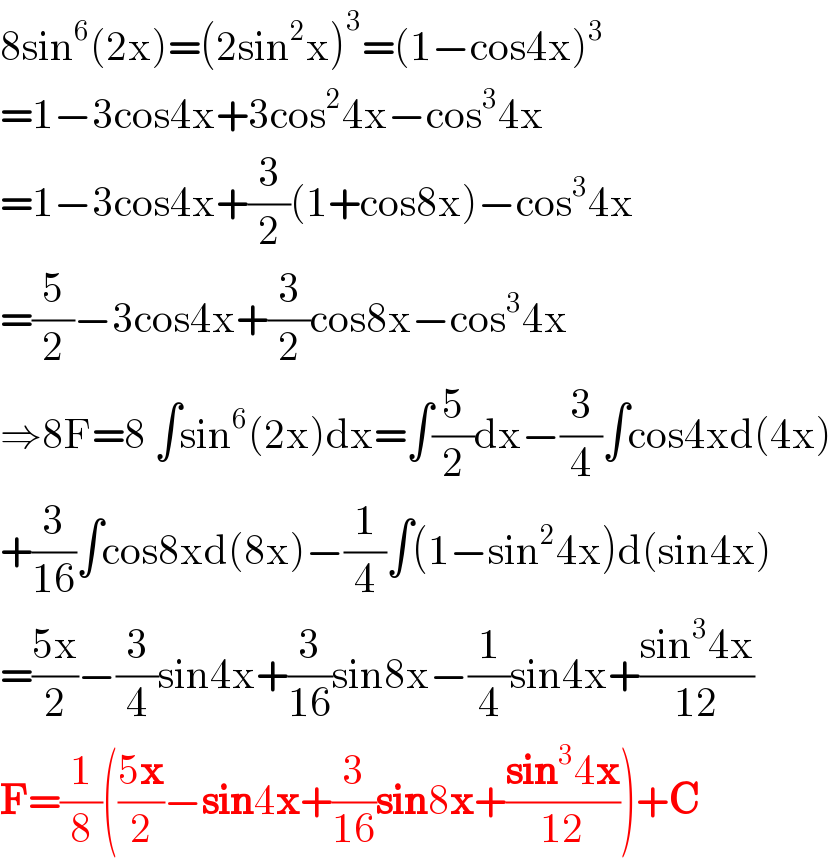
8sin^6 (2x)=(2sin^2 x)^3 =(1−cos4x)^3 =1−3cos4x+3cos^2 4x−cos^3 4x =1−3cos4x+(3/2)(1+cos8x)−cos^3 4x =(5/2)−3cos4x+(3/2)cos8x−cos^3 4x ⇒8F=8 ∫sin^6 (2x)dx=∫(5/2)dx−(3/4)∫cos4xd(4x) +(3/(16))∫cos8xd(8x)−(1/4)∫(1−sin^2 4x)d(sin4x) =((5x)/2)−(3/4)sin4x+(3/(16))sin8x−(1/4)sin4x+((sin^3 4x)/(12)) F=(1/8)(((5x)/2)−sin4x+(3/(16))sin8x+((sin^3 4x)/(12)))+C
$$\mathrm{8sin}^{\mathrm{6}} \left(\mathrm{2x}\right)=\left(\mathrm{2sin}^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{3}} =\left(\mathrm{1}−\mathrm{cos4x}\right)^{\mathrm{3}} \\ $$$$=\mathrm{1}−\mathrm{3cos4x}+\mathrm{3cos}^{\mathrm{2}} \mathrm{4x}−\mathrm{cos}^{\mathrm{3}} \mathrm{4x} \\ $$$$=\mathrm{1}−\mathrm{3cos4x}+\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{cos8x}\right)−\mathrm{cos}^{\mathrm{3}} \mathrm{4x} \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}−\mathrm{3cos4x}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{cos8x}−\mathrm{cos}^{\mathrm{3}} \mathrm{4x} \\ $$$$\Rightarrow\mathrm{8F}=\mathrm{8}\:\int\mathrm{sin}^{\mathrm{6}} \left(\mathrm{2x}\right)\mathrm{dx}=\int\frac{\mathrm{5}}{\mathrm{2}}\mathrm{dx}−\frac{\mathrm{3}}{\mathrm{4}}\int\mathrm{cos4xd}\left(\mathrm{4x}\right) \\ $$$$+\frac{\mathrm{3}}{\mathrm{16}}\int\mathrm{cos8xd}\left(\mathrm{8x}\right)−\frac{\mathrm{1}}{\mathrm{4}}\int\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{4x}\right)\mathrm{d}\left(\mathrm{sin4x}\right) \\ $$$$=\frac{\mathrm{5x}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{sin4x}+\frac{\mathrm{3}}{\mathrm{16}}\mathrm{sin8x}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin4x}+\frac{\mathrm{sin}^{\mathrm{3}} \mathrm{4x}}{\mathrm{12}} \\ $$$$\boldsymbol{\mathrm{F}}=\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{5}\boldsymbol{\mathrm{x}}}{\mathrm{2}}−\boldsymbol{\mathrm{sin}}\mathrm{4}\boldsymbol{\mathrm{x}}+\frac{\mathrm{3}}{\mathrm{16}}\boldsymbol{\mathrm{sin}}\mathrm{8}\boldsymbol{\mathrm{x}}+\frac{\boldsymbol{\mathrm{sin}}^{\mathrm{3}} \mathrm{4}\boldsymbol{\mathrm{x}}}{\mathrm{12}}\right)+\boldsymbol{\mathrm{C}}\: \\ $$
Answered by mathmax by abdo last updated on 16/Oct/20
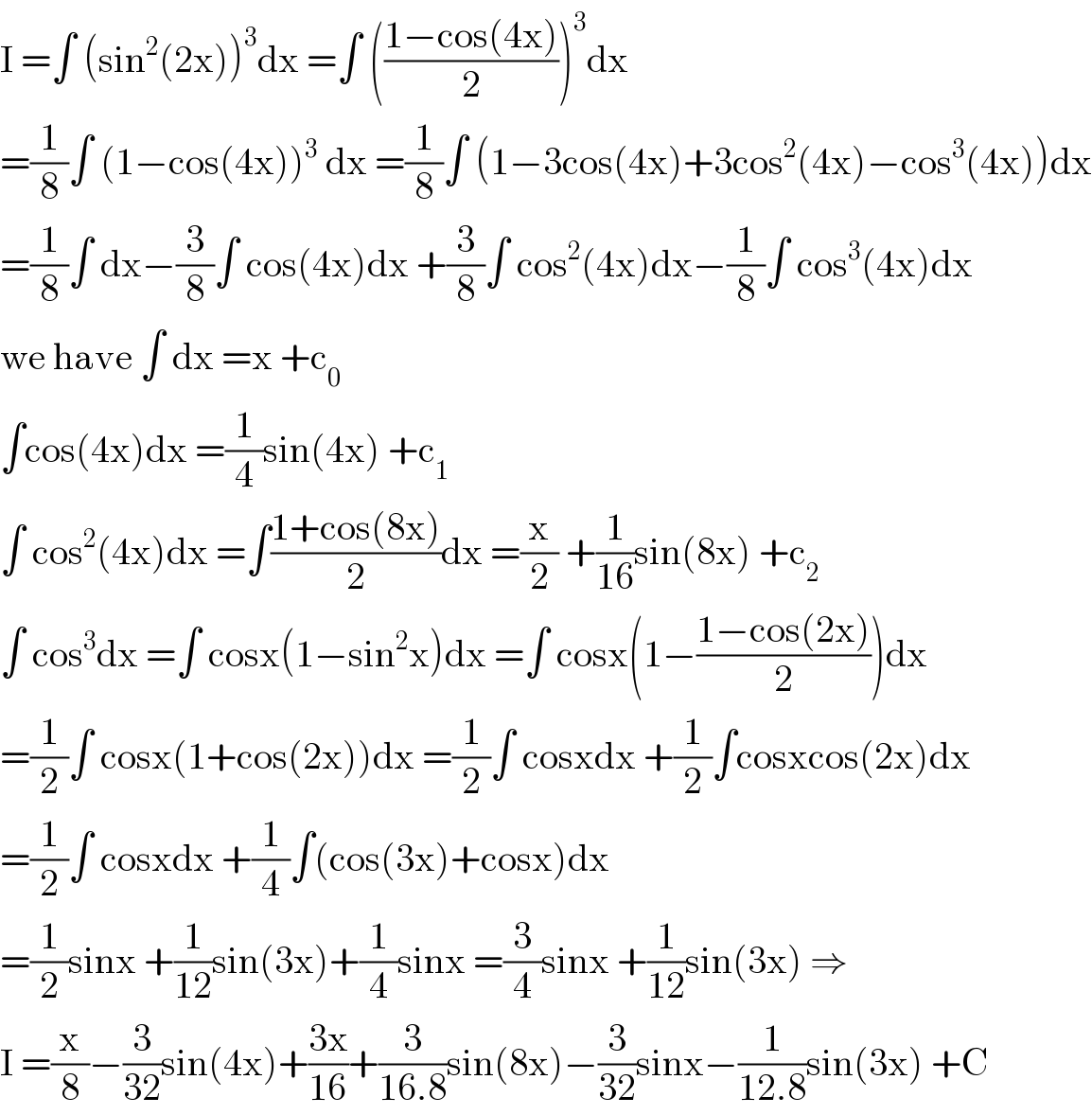
I =∫ (sin^2 (2x))^3 dx =∫ (((1−cos(4x))/2))^3 dx =(1/8)∫ (1−cos(4x))^3 dx =(1/8)∫ (1−3cos(4x)+3cos^2 (4x)−cos^3 (4x))dx =(1/8)∫ dx−(3/8)∫ cos(4x)dx +(3/8)∫ cos^2 (4x)dx−(1/8)∫ cos^3 (4x)dx we have ∫ dx =x +c_0 ∫cos(4x)dx =(1/4)sin(4x) +c_1 ∫ cos^2 (4x)dx =∫((1+cos(8x))/2)dx =(x/2) +(1/(16))sin(8x) +c_2 ∫ cos^3 dx =∫ cosx(1−sin^2 x)dx =∫ cosx(1−((1−cos(2x))/2))dx =(1/2)∫ cosx(1+cos(2x))dx =(1/2)∫ cosxdx +(1/2)∫cosxcos(2x)dx =(1/2)∫ cosxdx +(1/4)∫(cos(3x)+cosx)dx =(1/2)sinx +(1/(12))sin(3x)+(1/4)sinx =(3/4)sinx +(1/(12))sin(3x) ⇒ I =(x/8)−(3/(32))sin(4x)+((3x)/(16))+(3/(16.8))sin(8x)−(3/(32))sinx−(1/(12.8))sin(3x) +C
$$\mathrm{I}\:=\int\:\left(\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2x}\right)\right)^{\mathrm{3}} \mathrm{dx}\:=\int\:\left(\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{4x}\right)}{\mathrm{2}}\right)^{\mathrm{3}} \mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\:\left(\mathrm{1}−\mathrm{cos}\left(\mathrm{4x}\right)\right)^{\mathrm{3}} \:\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{8}}\int\:\left(\mathrm{1}−\mathrm{3cos}\left(\mathrm{4x}\right)+\mathrm{3cos}^{\mathrm{2}} \left(\mathrm{4x}\right)−\mathrm{cos}^{\mathrm{3}} \left(\mathrm{4x}\right)\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\:\mathrm{dx}−\frac{\mathrm{3}}{\mathrm{8}}\int\:\mathrm{cos}\left(\mathrm{4x}\right)\mathrm{dx}\:+\frac{\mathrm{3}}{\mathrm{8}}\int\:\mathrm{cos}^{\mathrm{2}} \left(\mathrm{4x}\right)\mathrm{dx}−\frac{\mathrm{1}}{\mathrm{8}}\int\:\mathrm{cos}^{\mathrm{3}} \left(\mathrm{4x}\right)\mathrm{dx} \\ $$$$\mathrm{we}\:\mathrm{have}\:\int\:\mathrm{dx}\:=\mathrm{x}\:+\mathrm{c}_{\mathrm{0}} \\ $$$$\int\mathrm{cos}\left(\mathrm{4x}\right)\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\left(\mathrm{4x}\right)\:+\mathrm{c}_{\mathrm{1}} \\ $$$$\int\:\mathrm{cos}^{\mathrm{2}} \left(\mathrm{4x}\right)\mathrm{dx}\:=\int\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{8x}\right)}{\mathrm{2}}\mathrm{dx}\:=\frac{\mathrm{x}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{16}}\mathrm{sin}\left(\mathrm{8x}\right)\:+\mathrm{c}_{\mathrm{2}} \\ $$$$\int\:\mathrm{cos}^{\mathrm{3}} \mathrm{dx}\:=\int\:\mathrm{cosx}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)\mathrm{dx}\:=\int\:\mathrm{cosx}\left(\mathrm{1}−\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\mathrm{cosx}\left(\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)\right)\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\mathrm{cosxdx}\:+\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{cosxcos}\left(\mathrm{2x}\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\mathrm{cosxdx}\:+\frac{\mathrm{1}}{\mathrm{4}}\int\left(\mathrm{cos}\left(\mathrm{3x}\right)+\mathrm{cosx}\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sinx}\:+\frac{\mathrm{1}}{\mathrm{12}}\mathrm{sin}\left(\mathrm{3x}\right)+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sinx}\:=\frac{\mathrm{3}}{\mathrm{4}}\mathrm{sinx}\:+\frac{\mathrm{1}}{\mathrm{12}}\mathrm{sin}\left(\mathrm{3x}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\mathrm{x}}{\mathrm{8}}−\frac{\mathrm{3}}{\mathrm{32}}\mathrm{sin}\left(\mathrm{4x}\right)+\frac{\mathrm{3x}}{\mathrm{16}}+\frac{\mathrm{3}}{\mathrm{16}.\mathrm{8}}\mathrm{sin}\left(\mathrm{8x}\right)−\frac{\mathrm{3}}{\mathrm{32}}\mathrm{sinx}−\frac{\mathrm{1}}{\mathrm{12}.\mathrm{8}}\mathrm{sin}\left(\mathrm{3x}\right)\:+\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *