Question Number 148454 by mathdanisur last updated on 28/Jul/21

$${sin}^{\mathrm{6}} \boldsymbol{\alpha}\:+\:{co}^{\mathrm{6}} \boldsymbol{\alpha}\:=\:\frac{\mathrm{3}}{\mathrm{4}}\:\:\Rightarrow\:\:\mathrm{6}{cos}\mathrm{4}\boldsymbol{\alpha}=? \\ $$$$ \\ $$
Answered by Ar Brandon last updated on 28/Jul/21
![sin^6 α+cos^6 α=(3/4) (sin^2 α+cos^2 α)[(sin^2 α+cos^2 α)^2 −3sin^2 αcos^2 α]=(3/4) 1−3sin^2 αcos^2 α=(3/4)⇒sin^2 αcos^2 α=(1/(12)) 6cos4α=6(cos^2 2α−sin^2 2α) 6cos4α=6[(cos^4 α−2sin^2 αcos^2 α+sin^4 α)−4sin^2 αcos^2 α] =6[(cos^2 α+sin^2 α)^2 −8sin^2 αcos^2 α] =6(1−8sin^2 αcos^2 α)=6(1−(8/(12)))=2](https://www.tinkutara.com/question/Q148462.png)
$$\mathrm{sin}^{\mathrm{6}} \alpha+\mathrm{cos}^{\mathrm{6}} \alpha=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\left(\mathrm{sin}^{\mathrm{2}} \alpha+\mathrm{cos}^{\mathrm{2}} \alpha\right)\left[\left(\mathrm{sin}^{\mathrm{2}} \alpha+\mathrm{cos}^{\mathrm{2}} \alpha\right)^{\mathrm{2}} −\mathrm{3sin}^{\mathrm{2}} \alpha\mathrm{cos}^{\mathrm{2}} \alpha\right]=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{1}−\mathrm{3sin}^{\mathrm{2}} \alpha\mathrm{cos}^{\mathrm{2}} \alpha=\frac{\mathrm{3}}{\mathrm{4}}\Rightarrow\mathrm{sin}^{\mathrm{2}} \alpha\mathrm{cos}^{\mathrm{2}} \alpha=\frac{\mathrm{1}}{\mathrm{12}} \\ $$$$\mathrm{6cos4}\alpha=\mathrm{6}\left(\mathrm{cos}^{\mathrm{2}} \mathrm{2}\alpha−\mathrm{sin}^{\mathrm{2}} \mathrm{2}\alpha\right) \\ $$$$\mathrm{6cos4}\alpha=\mathrm{6}\left[\left(\mathrm{cos}^{\mathrm{4}} \alpha−\mathrm{2sin}^{\mathrm{2}} \alpha\mathrm{cos}^{\mathrm{2}} \alpha+\mathrm{sin}^{\mathrm{4}} \alpha\right)−\mathrm{4sin}^{\mathrm{2}} \alpha\mathrm{cos}^{\mathrm{2}} \alpha\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{6}\left[\left(\mathrm{cos}^{\mathrm{2}} \alpha+\mathrm{sin}^{\mathrm{2}} \alpha\right)^{\mathrm{2}} −\mathrm{8sin}^{\mathrm{2}} \alpha\mathrm{cos}^{\mathrm{2}} \alpha\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{6}\left(\mathrm{1}−\mathrm{8sin}^{\mathrm{2}} \alpha\mathrm{cos}^{\mathrm{2}} \alpha\right)=\mathrm{6}\left(\mathrm{1}−\frac{\mathrm{8}}{\mathrm{12}}\right)=\mathrm{2} \\ $$
Commented by mathdanisur last updated on 28/Jul/21
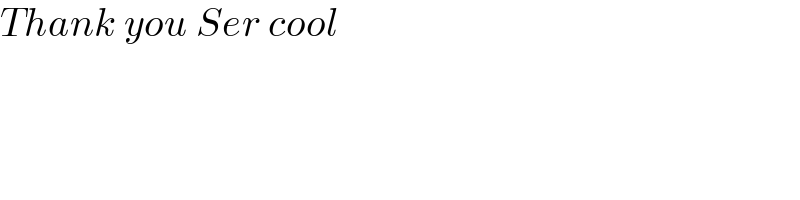
$${Thank}\:{you}\:{Ser}\:{cool} \\ $$
Answered by Olaf_Thorendsen last updated on 28/Jul/21

$$\mathrm{sin}^{\mathrm{6}} \alpha\:=\:\left(\frac{{e}^{{i}\alpha} −{e}^{−{i}\alpha} }{\mathrm{2}{i}}\right)^{\mathrm{6}} \\ $$$$\mathrm{sin}^{\mathrm{6}} \alpha\:=\:−\frac{\mathrm{1}}{\mathrm{64}}\left({e}^{\mathrm{6}{i}\alpha} −\mathrm{6}{e}^{{i}\mathrm{4}\alpha} +\mathrm{15}{e}^{{i}\mathrm{2}\alpha} −\mathrm{20}\right. \\ $$$$\left.+\mathrm{15}{e}^{−{i}\mathrm{2}\alpha} −\mathrm{6}{e}^{−{i}\mathrm{4}\alpha} +{e}^{−{i}\mathrm{6}\alpha} \right) \\ $$$$\mathrm{sin}^{\mathrm{6}} \alpha\:=\:−\frac{\mathrm{1}}{\mathrm{32}}\left(\mathrm{cos6}\alpha−\mathrm{6cos4}\alpha+\mathrm{15cos2}\alpha−\mathrm{10}\right) \\ $$$$ \\ $$$$\mathrm{cos}^{\mathrm{6}} \alpha\:=\:\left(\frac{{e}^{{i}\alpha} +{e}^{−{i}\alpha} }{\mathrm{2}}\right)^{\mathrm{6}} \\ $$$$\mathrm{cos}^{\mathrm{6}} \alpha\:=\:\frac{\mathrm{1}}{\mathrm{64}}\left({e}^{\mathrm{6}{i}\alpha} +\mathrm{6}{e}^{{i}\mathrm{4}\alpha} +\mathrm{15}{e}^{{i}\mathrm{2}\alpha} +\mathrm{20}\right. \\ $$$$\left.+\mathrm{15}{e}^{−{i}\mathrm{2}\alpha} +\mathrm{6}{e}^{−{i}\mathrm{4}\alpha} +{e}^{−{i}\mathrm{6}\alpha} \right) \\ $$$$\mathrm{cos}^{\mathrm{6}} \alpha\:=\:\frac{\mathrm{1}}{\mathrm{32}}\left(\mathrm{cos6}\alpha+\mathrm{6cos4}\alpha+\mathrm{15cos2}\alpha+\mathrm{10}\right) \\ $$$$ \\ $$$$\mathrm{sin}^{\mathrm{6}} \alpha+\mathrm{cos}^{\mathrm{6}} \alpha\:=\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\frac{\mathrm{1}}{\mathrm{32}}\left(\mathrm{12cos4}\alpha+\mathrm{20}\right)\:=\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{12cos4}\alpha\:=\:\frac{\mathrm{3}}{\mathrm{4}}×\mathrm{32}−\mathrm{20}\:=\:\mathrm{4} \\ $$$$\mathrm{6cos4}\alpha\:=\:\mathrm{2} \\ $$
Commented by mathdanisur last updated on 28/Jul/21
$${Thank}\:{you}\:{Ser}\:{cool} \\ $$
