Question Number 147809 by mathdanisur last updated on 23/Jul/21
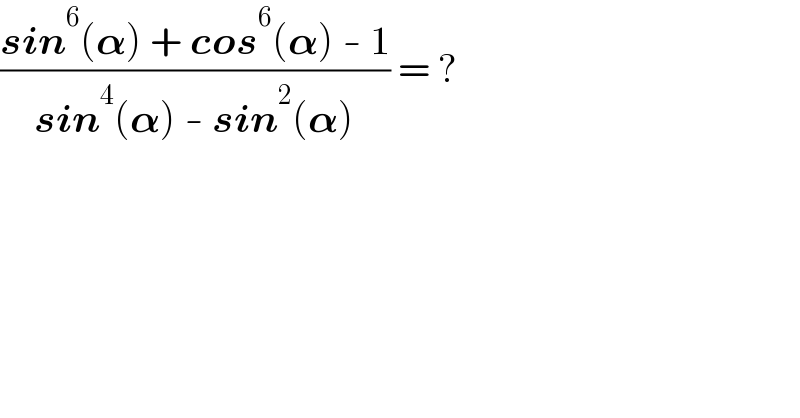
$$\frac{\boldsymbol{{sin}}^{\mathrm{6}} \left(\boldsymbol{\alpha}\right)\:+\:\boldsymbol{{cos}}^{\mathrm{6}} \left(\boldsymbol{\alpha}\right)\:-\:\mathrm{1}}{\boldsymbol{{sin}}^{\mathrm{4}} \left(\boldsymbol{\alpha}\right)\:-\:\boldsymbol{{sin}}^{\mathrm{2}} \left(\boldsymbol{\alpha}\right)}\:=\:? \\ $$
Answered by gsk2684 last updated on 23/Jul/21
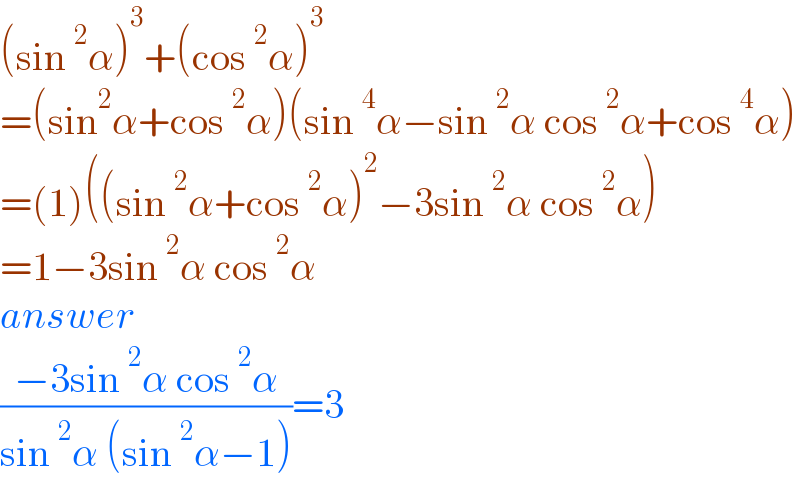
$$\left(\mathrm{sin}\:^{\mathrm{2}} \alpha\right)^{\mathrm{3}} +\left(\mathrm{cos}\:^{\mathrm{2}} \alpha\right)^{\mathrm{3}} \\ $$$$=\left(\mathrm{sin}^{\mathrm{2}} \alpha+\mathrm{cos}\:^{\mathrm{2}} \alpha\right)\left(\mathrm{sin}\:^{\mathrm{4}} \alpha−\mathrm{sin}\:^{\mathrm{2}} \alpha\:\mathrm{cos}\:^{\mathrm{2}} \alpha+\mathrm{cos}\:^{\mathrm{4}} \alpha\right) \\ $$$$=\left(\mathrm{1}\right)\left(\left(\mathrm{sin}\:^{\mathrm{2}} \alpha+\mathrm{cos}\:^{\mathrm{2}} \alpha\right)^{\mathrm{2}} −\mathrm{3sin}\:^{\mathrm{2}} \alpha\:\mathrm{cos}\:^{\mathrm{2}} \alpha\right) \\ $$$$=\mathrm{1}−\mathrm{3sin}\:^{\mathrm{2}} \alpha\:\mathrm{cos}\:^{\mathrm{2}} \alpha \\ $$$${answer} \\ $$$$\frac{−\mathrm{3sin}\:^{\mathrm{2}} \alpha\:\mathrm{cos}\:^{\mathrm{2}} \alpha}{\mathrm{sin}\:^{\mathrm{2}} \alpha\:\left(\mathrm{sin}\:^{\mathrm{2}} \alpha−\mathrm{1}\right)}=\mathrm{3} \\ $$
Commented by mathdanisur last updated on 23/Jul/21

$${Thank}\:{you}\:{Sir} \\ $$$${Answer}:\:\:\mathrm{3}\:{or}\:−\mathrm{3}.? \\ $$
Commented by puissant last updated on 23/Jul/21
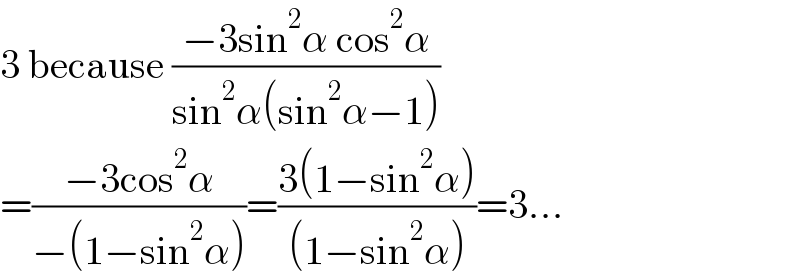
$$\mathrm{3}\:\mathrm{because}\:\frac{−\mathrm{3sin}^{\mathrm{2}} \alpha\:\mathrm{cos}^{\mathrm{2}} \alpha}{\mathrm{sin}^{\mathrm{2}} \alpha\left(\mathrm{sin}^{\mathrm{2}} \alpha−\mathrm{1}\right)} \\ $$$$=\frac{−\mathrm{3cos}^{\mathrm{2}} \alpha}{−\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \alpha\right)}=\frac{\mathrm{3}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \alpha\right)}{\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \alpha\right)}=\mathrm{3}… \\ $$
Commented by mathdanisur last updated on 23/Jul/21

$${thank}\:{you}\:{Sir} \\ $$
