Menu Close

sin-6-x-cos-6-x-sin-2-xcos-2-x-intregrate-

Tinku Tara 0 Comments
Pin




Question Number 49816 by Aditya789 last updated on 11/Dec/18
((sin^6 x−cos^6 x)/(sin^2 xcos^2 x)).intregrate
$$\frac{\mathrm{sin}^{\mathrm{6}} \mathrm{x}−\mathrm{cos}^{\mathrm{6}} \mathrm{x}}{\mathrm{sin}^{\mathrm{2}} \mathrm{xcos}^{\mathrm{2}} \mathrm{x}}.\mathrm{intregrate} \\ $$
Answered by AdqhK ÐQeQqQ last updated on 11/Dec/18
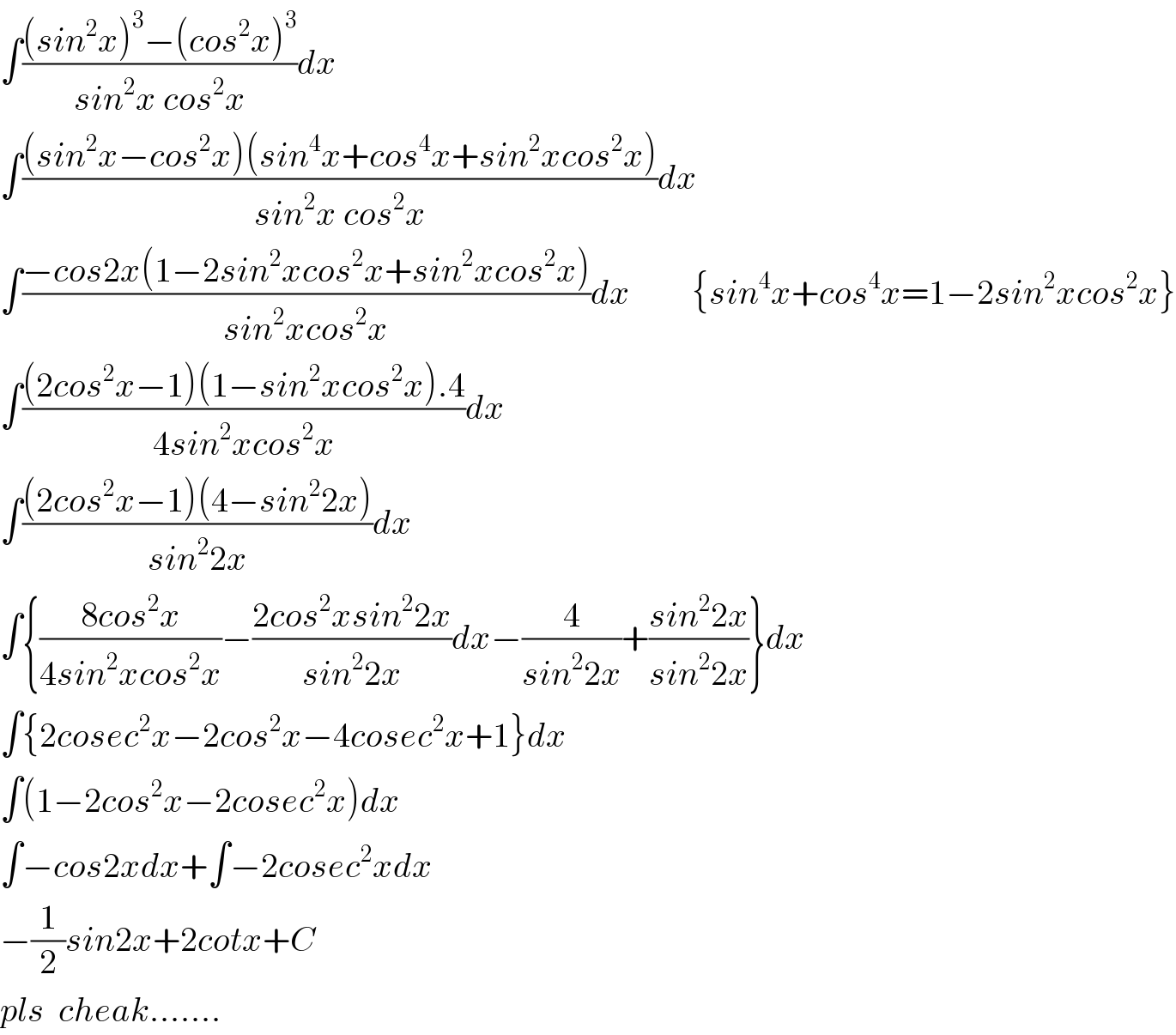
∫(((sin^2 x)^3 −(cos^2 x)^3 )/(sin^2 x cos^2 x))dx ∫(((sin^2 x−cos^2 x)(sin^4 x+cos^4 x+sin^2 xcos^2 x))/(sin^2 x cos^2 x))dx ∫((−cos2x(1−2sin^2 xcos^2 x+sin^2 xcos^2 x))/(sin^2 xcos^2 x))dx {sin^4 x+cos^4 x=1−2sin^2 xcos^2 x} ∫(((2cos^2 x−1)(1−sin^2 xcos^2 x).4)/(4sin^2 xcos^2 x))dx ∫(((2cos^2 x−1)(4−sin^2 2x))/(sin^2 2x))dx ∫{((8cos^2 x)/(4sin^2 xcos^2 x))−((2cos^2 xsin^2 2x)/(sin^2 2x))dx−(4/(sin^2 2x))+((sin^2 2x)/(sin^2 2x))}dx ∫{2cosec^2 x−2cos^2 x−4cosec^2 x+1}dx ∫(1−2cos^2 x−2cosec^2 x)dx ∫−cos2xdx+∫−2cosec^2 xdx −(1/2)sin2x+2cotx+C pls cheak.......
$$\int\frac{\left({sin}^{\mathrm{2}} {x}\right)^{\mathrm{3}} −\left({cos}^{\mathrm{2}} {x}\right)^{\mathrm{3}} }{{sin}^{\mathrm{2}} {x}\:{cos}^{\mathrm{2}} {x}}{dx} \\ $$$$\int\frac{\left({sin}^{\mathrm{2}} {x}−{cos}^{\mathrm{2}} {x}\right)\left({sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}+{sin}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}\right)}{{sin}^{\mathrm{2}} {x}\:{cos}^{\mathrm{2}} {x}}{dx} \\ $$$$\int\frac{−{cos}\mathrm{2}{x}\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}+{sin}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}\right)}{{sin}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}}{dx}\:\:\:\:\:\:\:\:\:\left\{{sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}=\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}\right\} \\ $$$$\int\frac{\left(\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{1}\right)\left(\mathrm{1}−{sin}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}\right).\mathrm{4}}{\mathrm{4}{sin}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}}{dx} \\ $$$$\int\frac{\left(\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{1}\right)\left(\mathrm{4}−{sin}^{\mathrm{2}} \mathrm{2}{x}\right)}{{sin}^{\mathrm{2}} \mathrm{2}{x}}{dx} \\ $$$$\int\left\{\frac{\mathrm{8}{cos}^{\mathrm{2}} {x}}{\mathrm{4}{sin}^{\mathrm{2}} {xcos}^{\mathrm{2}} {x}}−\frac{\mathrm{2}{cos}^{\mathrm{2}} {xsin}^{\mathrm{2}} \mathrm{2}{x}}{{sin}^{\mathrm{2}} \mathrm{2}{x}}{dx}−\frac{\mathrm{4}}{{sin}^{\mathrm{2}} \mathrm{2}{x}}+\frac{{sin}^{\mathrm{2}} \mathrm{2}{x}}{{sin}^{\mathrm{2}} \mathrm{2}{x}}\right\}{dx} \\ $$$$\int\left\{\mathrm{2}{cosec}^{\mathrm{2}} {x}−\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{4}{cosec}^{\mathrm{2}} {x}+\mathrm{1}\right\}{dx} \\ $$$$\int\left(\mathrm{1}−\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{2}{cosec}^{\mathrm{2}} {x}\right){dx} \\ $$$$\int−{cos}\mathrm{2}{xdx}+\int−\mathrm{2}{cosec}^{\mathrm{2}} {xdx} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}{x}+\mathrm{2}{cotx}+{C} \\ $$$${pls}\:\:{cheak}……. \\ $$
Commented by arvinddayama01@gmail.com. last updated on 11/Dec/18
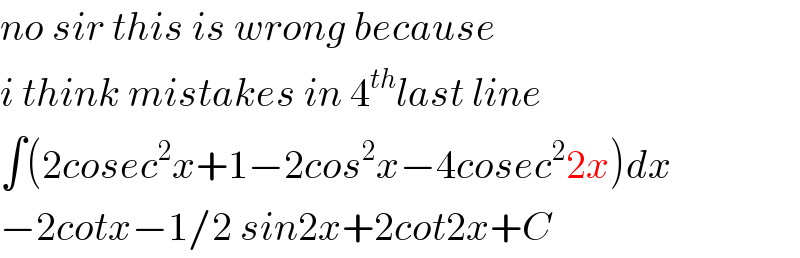
no sir this is wrong because i think mistakes in 4^(th) last line ∫(2cosec^2 x+1−2cos^2 x−4cosec^2 2x)dx −2cotx−1/2 sin2x+2cot2x+C
$${no}\:{sir}\:{this}\:{is}\:{wrong}\:{because} \\ $$$${i}\:{think}\:{mistakes}\:{in}\:\mathrm{4}^{{th}} {last}\:{line} \\ $$$$\int\left(\mathrm{2}{cosec}^{\mathrm{2}} {x}+\mathrm{1}−\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{4}{cosec}^{\mathrm{2}} \mathrm{2}{x}\right){dx} \\ $$$$−\mathrm{2}{cotx}−\mathrm{1}/\mathrm{2}\:{sin}\mathrm{2}{x}+\mathrm{2}{cot}\mathrm{2}{x}+{C} \\ $$
Commented by AdqhK ÐQeQqQ last updated on 11/Dec/18
sorry
$${sorry}\: \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 11/Dec/18
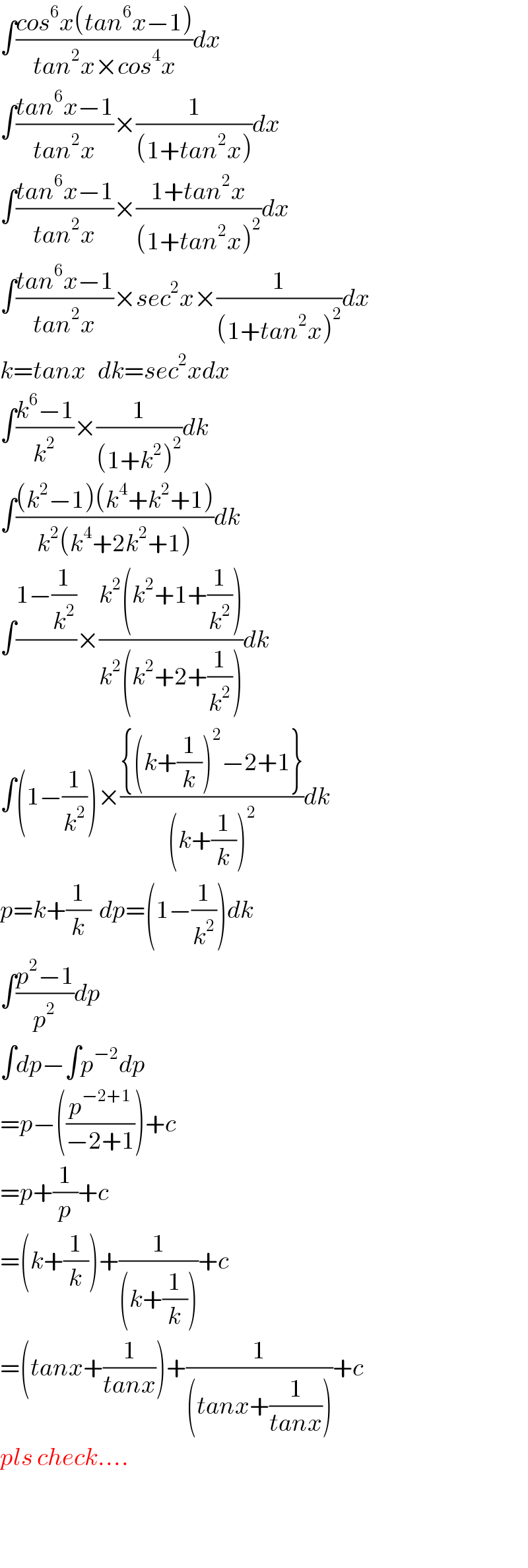
∫((cos^6 x(tan^6 x−1))/(tan^2 x×cos^4 x))dx ∫((tan^6 x−1)/(tan^2 x))×(1/((1+tan^2 x)))dx ∫((tan^6 x−1)/(tan^2 x))×((1+tan^2 x)/((1+tan^2 x)^2 ))dx ∫((tan^6 x−1)/(tan^2 x))×sec^2 x×(1/((1+tan^2 x)^2 ))dx k=tanx dk=sec^2 xdx ∫((k^6 −1)/k^2 )×(1/((1+k^2 )^2 ))dk ∫(((k^2 −1)(k^4 +k^2 +1))/(k^2 (k^4 +2k^2 +1)))dk ∫((1−(1/k^2 ))/)×((k^2 (k^2 +1+(1/k^2 )))/(k^2 (k^2 +2+(1/k^2 ))))dk ∫(1−(1/k^2 ))×(({(k+(1/k))^2 −2+1})/((k+(1/k))^2 ))dk p=k+(1/k) dp=(1−(1/k^2 ))dk ∫((p^2 −1)/p^2 )dp ∫dp−∫p^(−2) dp =p−((p^(−2+1) /(−2+1)))+c =p+(1/p)+c =(k+(1/k))+(1/((k+(1/k))))+c =(tanx+(1/(tanx)))+(1/((tanx+(1/(tanx)))))+c pls check....
$$\int\frac{{cos}^{\mathrm{6}} {x}\left({tan}^{\mathrm{6}} {x}−\mathrm{1}\right)}{{tan}^{\mathrm{2}} {x}×{cos}^{\mathrm{4}} {x}}{dx} \\ $$$$\int\frac{{tan}^{\mathrm{6}} {x}−\mathrm{1}}{{tan}^{\mathrm{2}} {x}}×\frac{\mathrm{1}}{\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)}{dx} \\ $$$$\int\frac{{tan}^{\mathrm{6}} {x}−\mathrm{1}}{{tan}^{\mathrm{2}} {x}}×\frac{\mathrm{1}+{tan}^{\mathrm{2}} {x}}{\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }{dx} \\ $$$$\int\frac{{tan}^{\mathrm{6}} {x}−\mathrm{1}}{{tan}^{\mathrm{2}} {x}}×{sec}^{\mathrm{2}} {x}×\frac{\mathrm{1}}{\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)^{\mathrm{2}} }{dx} \\ $$$${k}={tanx}\:\:\:{dk}={sec}^{\mathrm{2}} {xdx} \\ $$$$\int\frac{{k}^{\mathrm{6}} −\mathrm{1}}{{k}^{\mathrm{2}} }×\frac{\mathrm{1}}{\left(\mathrm{1}+{k}^{\mathrm{2}} \right)^{\mathrm{2}} }{dk} \\ $$$$\int\frac{\left({k}^{\mathrm{2}} −\mathrm{1}\right)\left({k}^{\mathrm{4}} +{k}^{\mathrm{2}} +\mathrm{1}\right)}{{k}^{\mathrm{2}} \left({k}^{\mathrm{4}} +\mathrm{2}{k}^{\mathrm{2}} +\mathrm{1}\right)}{dk} \\ $$$$\int\frac{\mathrm{1}−\frac{\mathrm{1}}{{k}^{\mathrm{2}} }}{}×\frac{{k}^{\mathrm{2}} \left({k}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\right)}{{k}^{\mathrm{2}} \left({k}^{\mathrm{2}} +\mathrm{2}+\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\right)}{dk} \\ $$$$\int\left(\mathrm{1}−\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\right)×\frac{\left\{\left({k}+\frac{\mathrm{1}}{{k}}\right)^{\mathrm{2}} −\mathrm{2}+\mathrm{1}\right\}}{\left({k}+\frac{\mathrm{1}}{{k}}\right)^{\mathrm{2}} }{dk} \\ $$$${p}={k}+\frac{\mathrm{1}}{{k}}\:\:{dp}=\left(\mathrm{1}−\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\right){dk} \\ $$$$\int\frac{{p}^{\mathrm{2}} −\mathrm{1}}{{p}^{\mathrm{2}} }{dp} \\ $$$$\int{dp}−\int{p}^{−\mathrm{2}} {dp} \\ $$$$={p}−\left(\frac{{p}^{−\mathrm{2}+\mathrm{1}} }{−\mathrm{2}+\mathrm{1}}\right)+{c} \\ $$$$={p}+\frac{\mathrm{1}}{{p}}+{c} \\ $$$$=\left({k}+\frac{\mathrm{1}}{{k}}\right)+\frac{\mathrm{1}}{\left({k}+\frac{\mathrm{1}}{{k}}\right)}+{c} \\ $$$$=\left({tanx}+\frac{\mathrm{1}}{{tanx}}\right)+\frac{\mathrm{1}}{\left({tanx}+\frac{\mathrm{1}}{{tanx}}\right)}+{c} \\ $$$${pls}\:{check}…. \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *