sin-7-x-x-7-dx-

Question Number 83367 by M±th+et£s last updated on 01/Mar/20

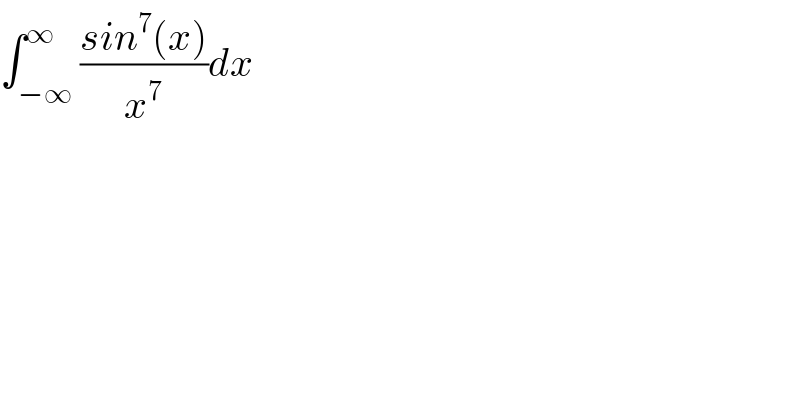
\int_{- \infty}^{\infty} \frac{{s i n}^{7} (x)}{x^{7}} d x

Commented by mathmax by abdo last updated on 02/Mar/20

t h i s i n t e g r a l i s s o l v a b l e b u t i f i n d a l o t s o f c a l c u l u s

I = \int_{- \infty}^{+ \infty} \frac{{s i n}^{7} x}{x^{7}} d x = 2 \int_{0}^{\infty} \frac{{s i n}^{7} x}{x^{7}} d x a n d b y p s r t s u^{^{'}} = x^{- 7} a n d v = {s i n}^{7} x

\frac{1}{2} I = {[- \frac{1}{6} x^{- 6} {s i n}^{7} x]}_{0}^{+ \infty} + \frac{7}{6} \int_{0}^{\infty} \frac{1}{x^{6}} c o s x {s i n}^{6} x d x

= \frac{7}{12} \int_{0}^{\infty} \frac{s i n (2 x) {s i n}^{4} x}{x^{6}} d x = \frac{7}{12} \int_{0}^{\infty} \frac{s i n (2 x)}{x^{6}} {(\frac{1 - c o s (2 x)}{2})}^{2} d x

= \frac{7}{48} \int_{0}^{\infty} \frac{s i n (2 x) (1 - 2 c o s (2 x) + {c o s}^{2} (2 x))}{x^{6}} d x

= \frac{7}{48} \int_{0}^{\infty} \frac{s i n (2 x)}{x^{6}} d x - \frac{14}{96} \int_{0}^{\infty} \frac{s i n (4 x)}{x^{6}} + \frac{7}{48} \int_{0}^{\infty} \frac{s i n (2 x) (\frac{1 + c o s (2 x)}{2})}{x^{6}} d x

\dots . . b e c o n t i n u e d \dots .