Question Number 119934 by bramlexs22 last updated on 28/Oct/20
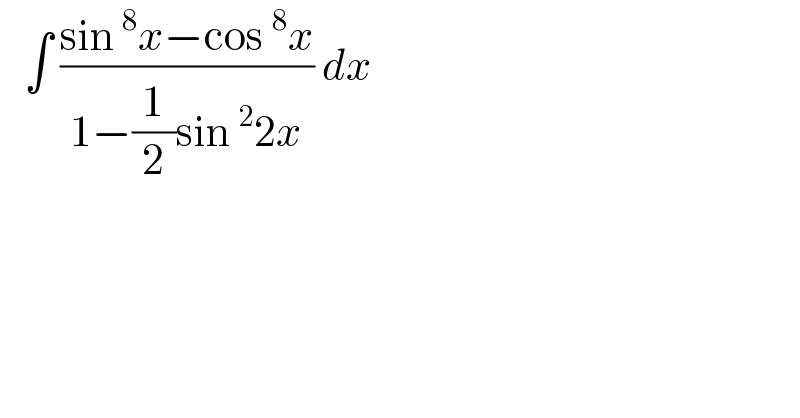
$$\:\:\:\int\:\frac{\mathrm{sin}\:^{\mathrm{8}} {x}−\mathrm{cos}\:^{\mathrm{8}} {x}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}}\:{dx}\: \\ $$
Answered by bobhans last updated on 28/Oct/20
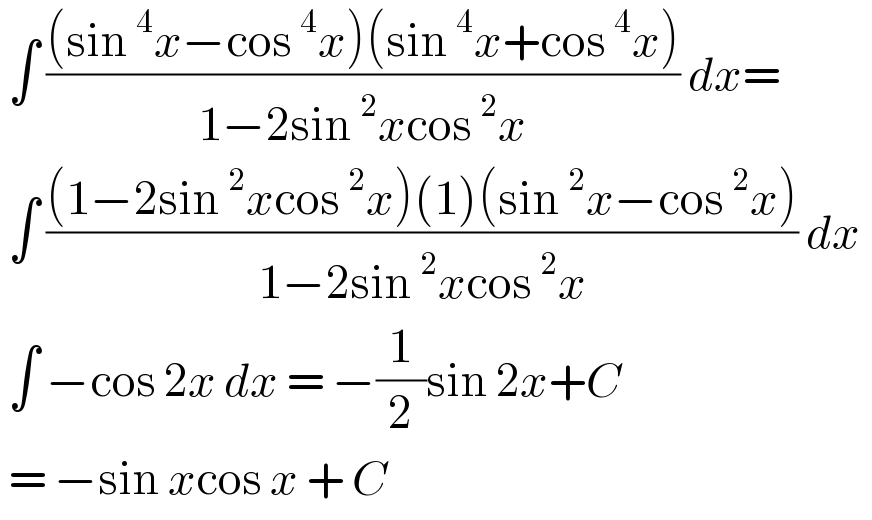
$$\:\int\:\frac{\left(\mathrm{sin}\:^{\mathrm{4}} {x}−\mathrm{cos}\:^{\mathrm{4}} {x}\right)\left(\mathrm{sin}\:^{\mathrm{4}} {x}+\mathrm{cos}\:^{\mathrm{4}} {x}\right)}{\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}\mathrm{cos}\:^{\mathrm{2}} {x}}\:{dx}= \\ $$$$\:\int\:\frac{\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}\mathrm{cos}\:^{\mathrm{2}} {x}\right)\left(\mathrm{1}\right)\left(\mathrm{sin}\:^{\mathrm{2}} {x}−\mathrm{cos}\:^{\mathrm{2}} {x}\right)}{\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}\mathrm{cos}\:^{\mathrm{2}} {x}}\:{dx}\overset{} {\:} \\ $$$$\:\int\:−\mathrm{cos}\:\mathrm{2}{x}\:{dx}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}{x}+{C} \\ $$$$\:=\:−\mathrm{sin}\:{x}\mathrm{cos}\:{x}\:+\:{C} \\ $$
Answered by mathmax by abdo last updated on 28/Oct/20
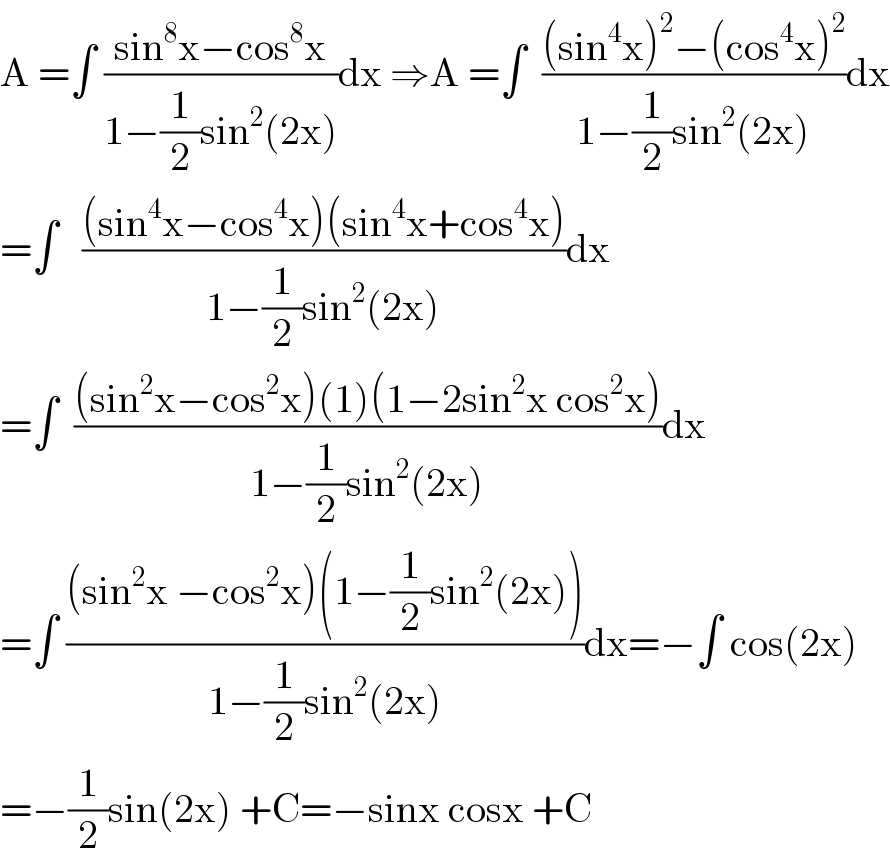
$$\mathrm{A}\:=\int\:\frac{\mathrm{sin}^{\mathrm{8}} \mathrm{x}−\mathrm{cos}^{\mathrm{8}} \mathrm{x}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2x}\right)}\mathrm{dx}\:\Rightarrow\mathrm{A}\:=\int\:\:\frac{\left(\mathrm{sin}^{\mathrm{4}} \mathrm{x}\right)^{\mathrm{2}} −\left(\mathrm{cos}^{\mathrm{4}} \mathrm{x}\right)^{\mathrm{2}} }{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2x}\right)}\mathrm{dx} \\ $$$$=\int\:\:\:\frac{\left(\mathrm{sin}^{\mathrm{4}} \mathrm{x}−\mathrm{cos}^{\mathrm{4}} \mathrm{x}\right)\left(\mathrm{sin}^{\mathrm{4}} \mathrm{x}+\mathrm{cos}^{\mathrm{4}} \mathrm{x}\right)}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2x}\right)}\mathrm{dx} \\ $$$$=\int\:\:\frac{\left(\mathrm{sin}^{\mathrm{2}} \mathrm{x}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{1}\right)\left(\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \mathrm{x}\:\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2x}\right)}\mathrm{dx} \\ $$$$=\int\:\frac{\left(\mathrm{sin}^{\mathrm{2}} \mathrm{x}\:−\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2x}\right)\right)}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2x}\right)}\mathrm{dx}=−\int\:\mathrm{cos}\left(\mathrm{2x}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2x}\right)\:+\mathrm{C}=−\mathrm{sinx}\:\mathrm{cosx}\:+\mathrm{C} \\ $$
