Question Number 160645 by tounghoungko last updated on 03/Dec/21
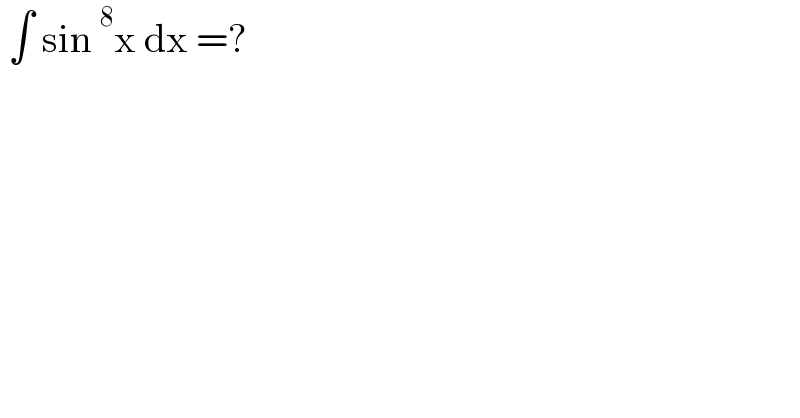
$$\:\int\:\mathrm{sin}\:^{\mathrm{8}} \mathrm{x}\:\mathrm{dx}\:=? \\ $$
Commented by swamy1234 last updated on 04/Dec/21
good
Answered by puissant last updated on 04/Dec/21

$$\Omega=\int{sin}^{\mathrm{8}} {x}\:{dx}\:\: \\ $$$${sin}^{\mathrm{8}} {x}\:=\:\left(\frac{{e}^{{ix}} −{e}^{−{ix}} }{\mathrm{2}{i}}\right)^{\mathrm{8}} =\:\frac{\mathrm{1}}{\mathrm{256}}\left({e}^{{ix}} −{e}^{−{ix}} \right)^{\mathrm{8}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{256}}\left\{{e}^{\mathrm{8}{ix}} −\mathrm{8}{e}^{\mathrm{7}{ix}} {e}^{−{ix}} +\mathrm{28}{e}^{\mathrm{6}{ix}} {e}^{−\mathrm{2}{ix}} −\mathrm{56}{e}^{\mathrm{5}{ix}} {e}^{−\mathrm{3}{ix}} +\mathrm{70}{e}^{{i}\mathrm{4}{x}} {e}^{−{i}\mathrm{4}{x}} \right. \\ $$$$\left.−\mathrm{56}{e}^{{i}\mathrm{3}{x}} {e}^{−{i}\mathrm{5}{x}} +\mathrm{28}{e}^{{i}\mathrm{2}{x}} {e}^{−{i}\mathrm{6}{x}} −\mathrm{8}{e}^{{ix}} {e}^{−{i}\mathrm{7}{x}} +{e}^{−{i}\mathrm{8}{x}} \right\} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{256}}\left\{\left({e}^{{i}\mathrm{8}{x}} +{e}^{−{i}\mathrm{8}{x}} \right)−\mathrm{8}\left({e}^{{i}\mathrm{6}{x}} +{e}^{−{i}\mathrm{6}{x}} \right)+\mathrm{28}\left({e}^{{i}\mathrm{4}{x}} +{e}^{−{i}\mathrm{4}{x}} \right)\right. \\ $$$$\left.−\mathrm{56}\left({e}^{{i}\mathrm{2}{x}} +{e}^{−\mathrm{2}{x}} \right)+\mathrm{70}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{128}}{cos}\mathrm{8}{x}−\frac{\mathrm{1}}{\mathrm{16}}{cos}\mathrm{6}{x}+\frac{\mathrm{7}}{\mathrm{32}}{cos}\mathrm{4}{x}−\frac{\mathrm{7}}{\mathrm{16}}{cos}\mathrm{2}{x}+\frac{\mathrm{35}}{\mathrm{128}} \\ $$$$\Omega\:=\:\int{sin}^{\mathrm{8}} {x}\:{dx}\:; \\ $$$$\Rightarrow\:\Omega\:=\:\frac{\mathrm{1}}{\mathrm{984}}{cos}\mathrm{8}{x}−\frac{\mathrm{1}}{\mathrm{96}}{cos}\mathrm{6}{x}+\frac{\mathrm{7}}{\mathrm{128}}{cos}\mathrm{4}{x}−\frac{\mathrm{7}}{\mathrm{32}}{cos}\mathrm{2}{x}+\frac{\mathrm{35}{x}}{\mathrm{128}}+{C}\:\left({C}\in\mathbb{R}\right) \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:………………..\mathscr{L}{e}\:{puissant}………………… \\ $$
Answered by peter frank last updated on 06/Dec/21
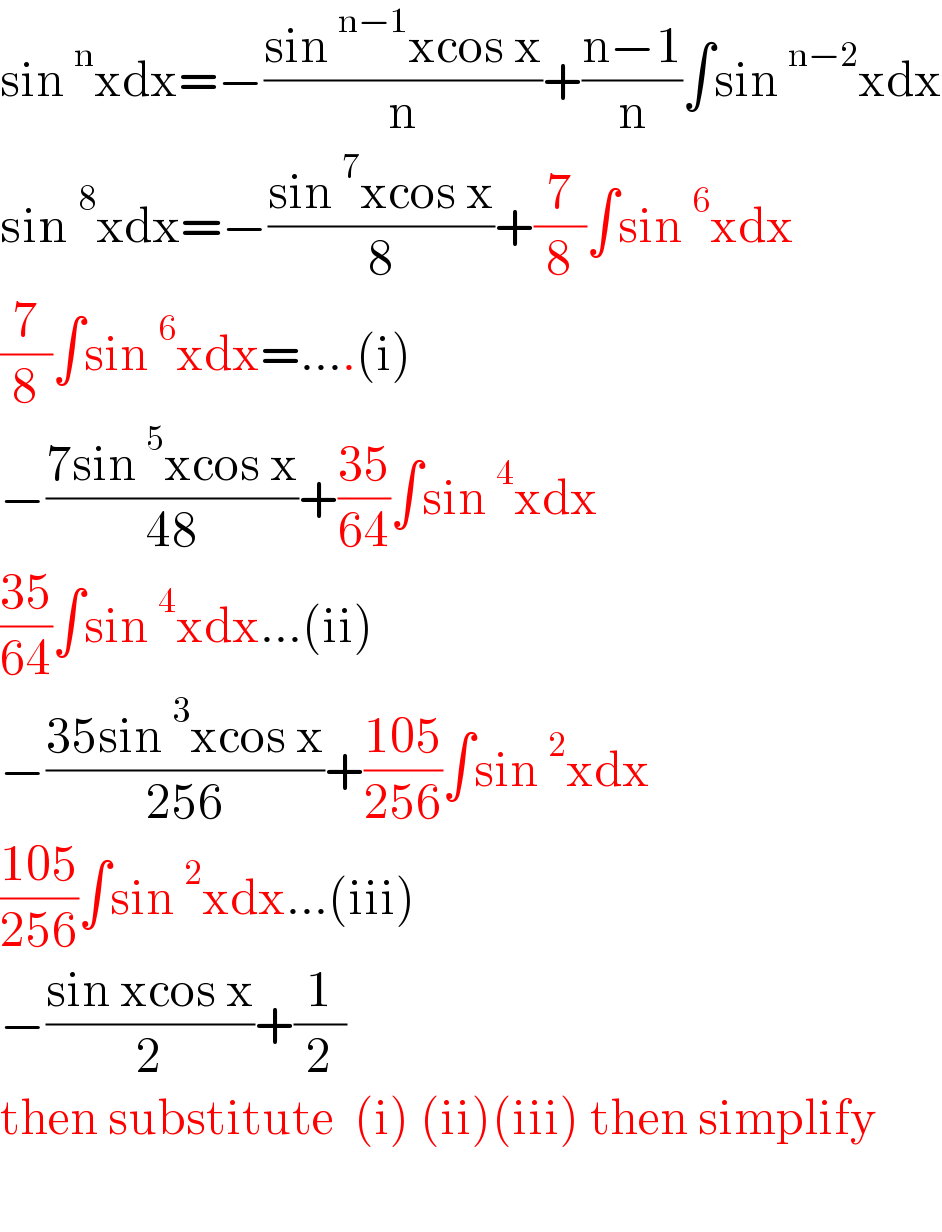
$$\mathrm{sin}\:^{\mathrm{n}} \mathrm{xdx}=−\frac{\mathrm{sin}\:^{\mathrm{n}−\mathrm{1}} \mathrm{xcos}\:\mathrm{x}}{\mathrm{n}}+\frac{\mathrm{n}−\mathrm{1}}{\mathrm{n}}\int\mathrm{sin}\:^{\mathrm{n}−\mathrm{2}} \mathrm{xdx} \\ $$$$\mathrm{sin}\:^{\mathrm{8}} \mathrm{xdx}=−\frac{\mathrm{sin}\:^{\mathrm{7}} \mathrm{xcos}\:\mathrm{x}}{\mathrm{8}}+\frac{\mathrm{7}}{\mathrm{8}}\int\mathrm{sin}\:^{\mathrm{6}} \mathrm{xdx} \\ $$$$\frac{\mathrm{7}}{\mathrm{8}}\int\mathrm{sin}\:^{\mathrm{6}} \mathrm{xdx}=….\left(\mathrm{i}\right) \\ $$$$−\frac{\mathrm{7sin}\:^{\mathrm{5}} \mathrm{xcos}\:\mathrm{x}}{\mathrm{48}}+\frac{\mathrm{35}}{\mathrm{64}}\int\mathrm{sin}\:^{\mathrm{4}} \mathrm{xdx} \\ $$$$\frac{\mathrm{35}}{\mathrm{64}}\int\mathrm{sin}\:^{\mathrm{4}} \mathrm{xdx}…\left(\mathrm{ii}\right) \\ $$$$−\frac{\mathrm{35sin}\:^{\mathrm{3}} \mathrm{xcos}\:\mathrm{x}}{\mathrm{256}}+\frac{\mathrm{105}}{\mathrm{256}}\int\mathrm{sin}\:^{\mathrm{2}} \mathrm{xdx} \\ $$$$\frac{\mathrm{105}}{\mathrm{256}}\int\mathrm{sin}\:^{\mathrm{2}} \mathrm{xdx}…\left(\mathrm{iii}\right) \\ $$$$−\frac{\mathrm{sin}\:\mathrm{xcos}\:\mathrm{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{then}\:\mathrm{substitute}\:\:\left(\mathrm{i}\right)\:\left(\mathrm{ii}\right)\left(\mathrm{iii}\right)\:\mathrm{then}\:\mathrm{simplify} \\ $$$$ \\ $$
