Question Number 112672 by bemath last updated on 09/Sep/20
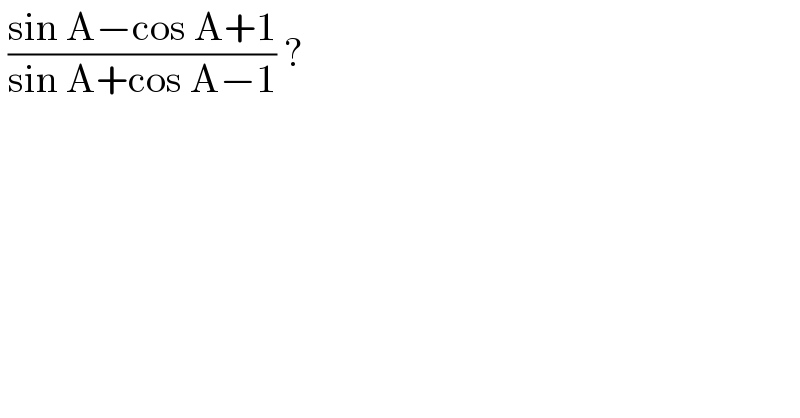
$$\:\frac{\mathrm{sin}\:\mathrm{A}−\mathrm{cos}\:\mathrm{A}+\mathrm{1}}{\mathrm{sin}\:\mathrm{A}+\mathrm{cos}\:\mathrm{A}−\mathrm{1}}\:?\: \\ $$
Commented by som(math1967) last updated on 09/Sep/20

$$\frac{\mathrm{1}+\mathrm{sinA}}{\mathrm{cosA}} \\ $$
Commented by bemath last updated on 09/Sep/20
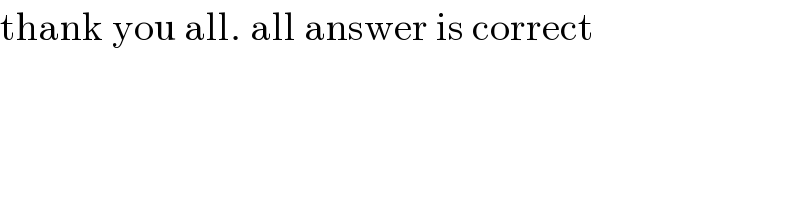
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{all}.\:\mathrm{all}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{correct} \\ $$
Answered by bobhans last updated on 09/Sep/20

$$\left(\blacklozenge\right)\frac{\left(\mathrm{sin}\:\mathrm{A}−\mathrm{cos}\:\mathrm{A}\right)+\mathrm{1}}{\left(\mathrm{sin}\:\mathrm{A}+\mathrm{cos}\:\mathrm{A}\right)−\mathrm{1}}\:×\frac{\left(\mathrm{sin}\:\mathrm{A}+\mathrm{cos}\:\mathrm{A}\right)+\mathrm{1}}{\left(\mathrm{sin}\:\mathrm{A}+\mathrm{cos}\:\mathrm{A}\right)+\mathrm{1}}\:= \\ $$$$\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{A}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{A}+\mathrm{sin}\:\mathrm{A}−\mathrm{cos}\:\mathrm{A}+\mathrm{sin}\:\mathrm{A}+\mathrm{cos}\:\mathrm{A}+\mathrm{1}}{\mathrm{1}+\mathrm{2sin}\:\mathrm{Acos}\:\mathrm{A}−\mathrm{1}}\:= \\ $$$$\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{A}−\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{A}\right)+\mathrm{2sin}\:\mathrm{A}+\mathrm{1}}{\mathrm{2sin}\:\mathrm{Acos}\:\mathrm{A}}\:= \\ $$$$\frac{\mathrm{2sin}\:^{\mathrm{2}} \mathrm{A}+\mathrm{2sin}\:\mathrm{A}}{\mathrm{2sin}\:\mathrm{Acos}\:\mathrm{A}}\:=\:\frac{\mathrm{2sin}\:\mathrm{A}\left(\mathrm{sin}\:\mathrm{A}+\mathrm{1}\right)}{\mathrm{2sin}\:\mathrm{Acos}\:\mathrm{A}} \\ $$$$=\:\frac{\mathrm{sin}\:\mathrm{A}+\mathrm{1}}{\mathrm{cos}\:\mathrm{A}}\:\mathrm{or}\:\frac{\mathrm{sin}\:\mathrm{A}+\mathrm{1}}{\mathrm{cos}\:\mathrm{A}}\:×\frac{\mathrm{sin}\:\mathrm{A}−\mathrm{1}}{\mathrm{sin}\:\mathrm{A}−\mathrm{1}} \\ $$$$=\:\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{A}−\mathrm{1}}{\mathrm{cos}\:\mathrm{A}\left(\mathrm{sin}\:\mathrm{A}−\mathrm{1}\right)}\:=\:\frac{\mathrm{cos}\:\mathrm{A}}{\mathrm{1}−\mathrm{sin}\:\mathrm{A}} \\ $$
Commented by som(math1967) last updated on 09/Sep/20
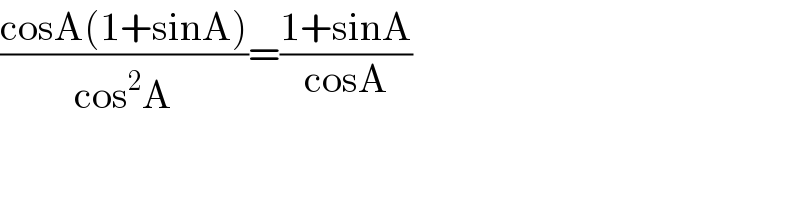
$$\frac{\mathrm{cosA}\left(\mathrm{1}+\mathrm{sinA}\right)}{\mathrm{cos}^{\mathrm{2}} \mathrm{A}}=\frac{\mathrm{1}+\mathrm{sinA}}{\mathrm{cosA}} \\ $$
Commented by bemath last updated on 09/Sep/20

$$\mathrm{same}\:\mathrm{sir}.\:\frac{\mathrm{1}+\mathrm{sin}\:\mathrm{A}}{\mathrm{cos}\:\mathrm{A}}\:=\:\frac{\mathrm{cos}\:\mathrm{A}}{\mathrm{1}−\mathrm{sin}\:\mathrm{A}} \\ $$
Commented by som(math1967) last updated on 09/Sep/20

$$\mathrm{yes}\:\mathrm{sir} \\ $$
Answered by Dwaipayan Shikari last updated on 09/Sep/20
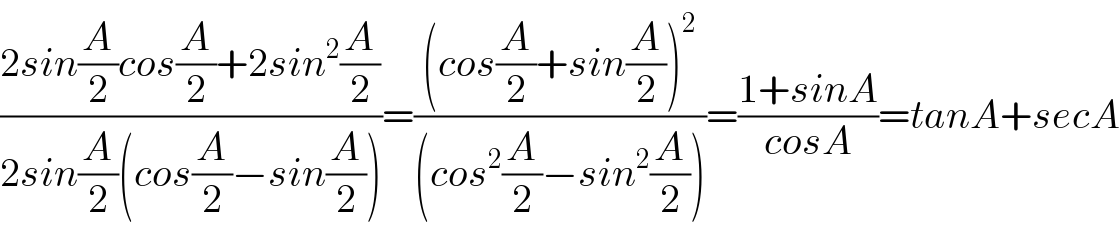
$$\frac{\mathrm{2}{sin}\frac{{A}}{\mathrm{2}}{cos}\frac{{A}}{\mathrm{2}}+\mathrm{2}{sin}^{\mathrm{2}} \frac{{A}}{\mathrm{2}}}{\mathrm{2}{sin}\frac{{A}}{\mathrm{2}}\left({cos}\frac{{A}}{\mathrm{2}}−{sin}\frac{{A}}{\mathrm{2}}\right)}=\frac{\left({cos}\frac{{A}}{\mathrm{2}}+{sin}\frac{{A}}{\mathrm{2}}\right)^{\mathrm{2}} }{\left({cos}^{\mathrm{2}} \frac{{A}}{\mathrm{2}}−{sin}^{\mathrm{2}} \frac{{A}}{\mathrm{2}}\right)}=\frac{\mathrm{1}+{sinA}}{{cosA}}={tanA}+{secA} \\ $$
