Menu Close

sin-a-sin-b-1-3-cos-a-cos-b-5-3-cos-2-a-b-

Tinku Tara 0 Comments
Pin




Question Number 129360 by bramlexs22 last updated on 15/Jan/21
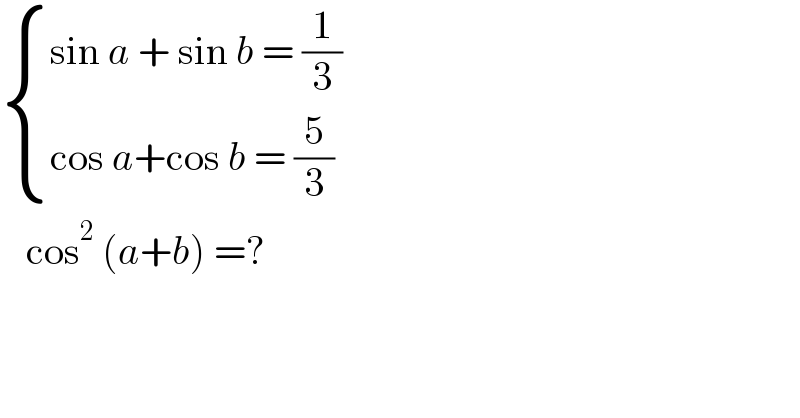
{ ((sin a + sin b = (1/3))),((cos a+cos b = (5/3))) :} cos^2 (a+b) =?
$$\begin{cases}{\mathrm{sin}\:{a}\:+\:\mathrm{sin}\:{b}\:=\:\frac{\mathrm{1}}{\mathrm{3}}}\\{\mathrm{cos}\:{a}+\mathrm{cos}\:{b}\:=\:\frac{\mathrm{5}}{\mathrm{3}}}\end{cases} \\ $$$$\:\:\:\:\mathrm{cos}^{\mathrm{2}} \:\left({a}+{b}\right)\:=?\: \\ $$
Commented by bramlexs22 last updated on 15/Jan/21
nice trigonometry
$$\:\mathrm{nice}\:\mathrm{trigonometry} \\ $$
Answered by liberty last updated on 15/Jan/21
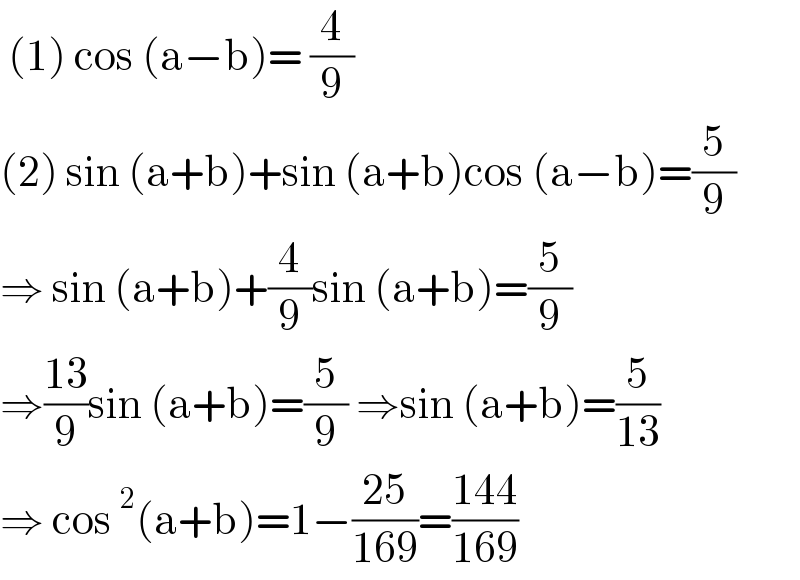
(1) cos (a−b)= (4/9) (2) sin (a+b)+sin (a+b)cos (a−b)=(5/9) ⇒ sin (a+b)+(4/9)sin (a+b)=(5/9) ⇒((13)/9)sin (a+b)=(5/9) ⇒sin (a+b)=(5/(13)) ⇒ cos^2 (a+b)=1−((25)/(169))=((144)/(169))
$$\:\left(\mathrm{1}\right)\:\mathrm{cos}\:\left(\mathrm{a}−\mathrm{b}\right)=\:\frac{\mathrm{4}}{\mathrm{9}} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{sin}\:\left(\mathrm{a}+\mathrm{b}\right)+\mathrm{sin}\:\left(\mathrm{a}+\mathrm{b}\right)\mathrm{cos}\:\left(\mathrm{a}−\mathrm{b}\right)=\frac{\mathrm{5}}{\mathrm{9}} \\ $$$$\Rightarrow\:\mathrm{sin}\:\left(\mathrm{a}+\mathrm{b}\right)+\frac{\mathrm{4}}{\mathrm{9}}\mathrm{sin}\:\left(\mathrm{a}+\mathrm{b}\right)=\frac{\mathrm{5}}{\mathrm{9}} \\ $$$$\Rightarrow\frac{\mathrm{13}}{\mathrm{9}}\mathrm{sin}\:\left(\mathrm{a}+\mathrm{b}\right)=\frac{\mathrm{5}}{\mathrm{9}}\:\Rightarrow\mathrm{sin}\:\left(\mathrm{a}+\mathrm{b}\right)=\frac{\mathrm{5}}{\mathrm{13}} \\ $$$$\Rightarrow\:\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{a}+\mathrm{b}\right)=\mathrm{1}−\frac{\mathrm{25}}{\mathrm{169}}=\frac{\mathrm{144}}{\mathrm{169}} \\ $$
Answered by bramlexs22 last updated on 15/Jan/21
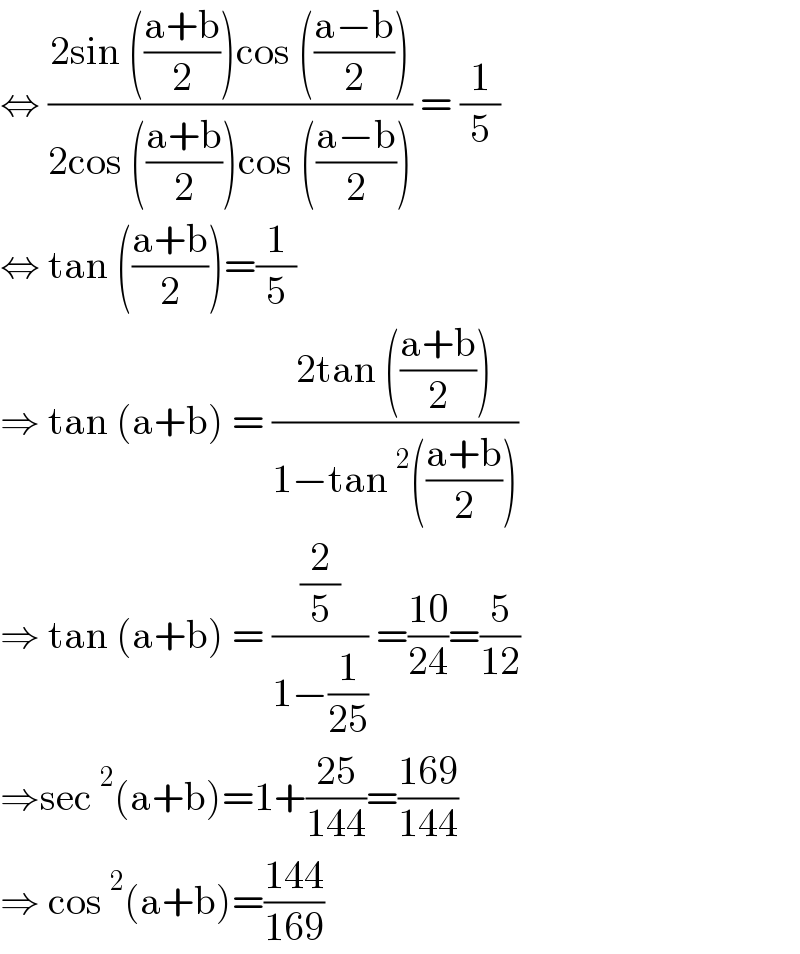
⇔ ((2sin (((a+b)/2))cos (((a−b)/2)))/(2cos (((a+b)/2))cos (((a−b)/2)))) = (1/5) ⇔ tan (((a+b)/2))=(1/5) ⇒ tan (a+b) = ((2tan (((a+b)/2)))/(1−tan^2 (((a+b)/2)))) ⇒ tan (a+b) = ((2/5)/(1−(1/(25)))) =((10)/(24))=(5/(12)) ⇒sec^2 (a+b)=1+((25)/(144))=((169)/(144)) ⇒ cos^2 (a+b)=((144)/(169))
$$\Leftrightarrow\:\frac{\mathrm{2sin}\:\left(\frac{\mathrm{a}+\mathrm{b}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\mathrm{a}−\mathrm{b}}{\mathrm{2}}\right)}{\mathrm{2cos}\:\left(\frac{\mathrm{a}+\mathrm{b}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\mathrm{a}−\mathrm{b}}{\mathrm{2}}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\Leftrightarrow\:\mathrm{tan}\:\left(\frac{\mathrm{a}+\mathrm{b}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\Rightarrow\:\mathrm{tan}\:\left(\mathrm{a}+\mathrm{b}\right)\:=\:\frac{\mathrm{2tan}\:\left(\frac{\mathrm{a}+\mathrm{b}}{\mathrm{2}}\right)}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\mathrm{a}+\mathrm{b}}{\mathrm{2}}\right)} \\ $$$$\Rightarrow\:\mathrm{tan}\:\left(\mathrm{a}+\mathrm{b}\right)\:=\:\frac{\frac{\mathrm{2}}{\mathrm{5}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{25}}}\:=\frac{\mathrm{10}}{\mathrm{24}}=\frac{\mathrm{5}}{\mathrm{12}} \\ $$$$\Rightarrow\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{a}+\mathrm{b}\right)=\mathrm{1}+\frac{\mathrm{25}}{\mathrm{144}}=\frac{\mathrm{169}}{\mathrm{144}} \\ $$$$\Rightarrow\:\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{a}+\mathrm{b}\right)=\frac{\mathrm{144}}{\mathrm{169}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *