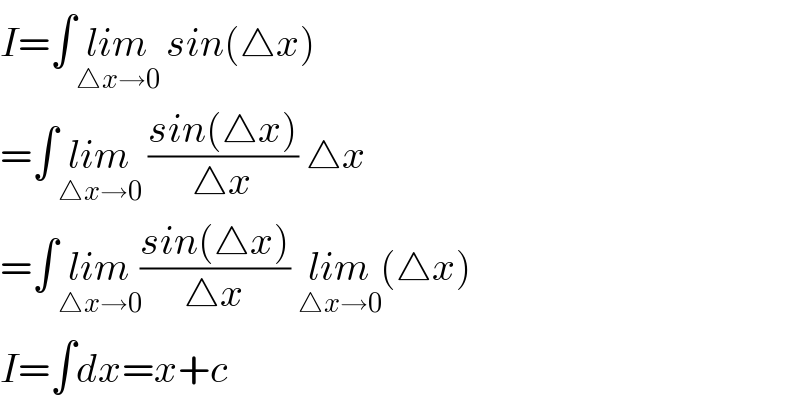sin-dx-

sin-dx-

Question Number 90198 by M±th+et£s last updated on 21/Apr/20

\int s i n (d x)

Commented by mr W last updated on 22/Apr/20

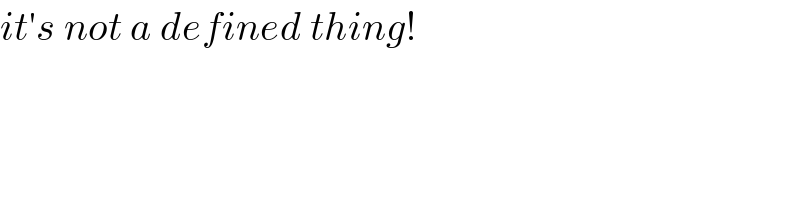
{i t}^{'} s n o t a d e f i n e d t h i n g!

Commented by M±th+et£s last updated on 22/Apr/20

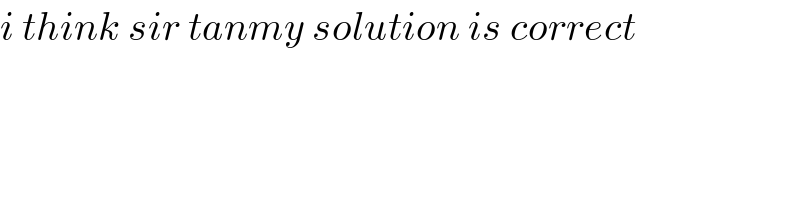
i t h i n k s i r t a n m y s o l u t i o n i s c o r r e c t

Commented by mr W last updated on 22/Apr/20

a s i s a i d t h i n g s l i k e \int f (d x) {d o n}^{'} t

e x i s t b e c a u s e t h e y a r e n o t d e f i n e d .

d x i s n o t a v a r i a b l e o r a v a l u e .

\int f (x) d x i s d e f i n e d a s :

\int f (x) d x = F (x) \equiv \frac{d F (x)}{d x} = f (x)

b o t h \int a n d d x a r e j u s t s y m b o l s .

c a n y o u t e l l w h a t \int f (d x) m e a n s ?

Answered by frc2crc last updated on 22/Apr/20

i t x + C

Commented by M±th+et£s last updated on 22/Apr/20

y e s

Answered by TANMAY PANACEA. last updated on 22/Apr/20

s i n (d x) \approx d x

\int d x

= x + c

Answered by M±th+et£s last updated on 22/Apr/20

I = \int \underset{△ x \to 0}{l i m} s i n (△ x)

= \int \underset{△ x \to 0}{l i m} \frac{s i n (△ x)}{△ x} △ x

= \int \underset{△ x \to 0}{l i m} \frac{s i n (△ x)}{△ x} \underset{△ x \to 0}{l i m} (△ x)

I = \int d x = x + c