Question Number 156695 by amin96 last updated on 14/Oct/21
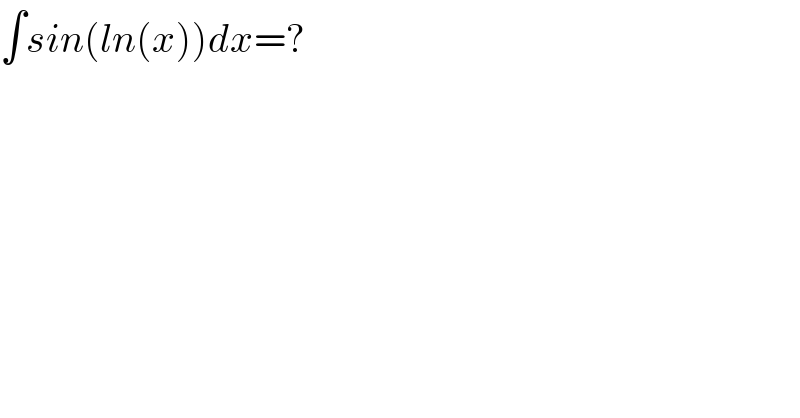
$$\int{sin}\left({ln}\left({x}\right)\right){dx}=? \\ $$
Answered by puissant last updated on 10/Nov/21
![Q=∫_0 ^1 sin(lnx)dx ; u=lnx→x=e^u →dx=e^u du ⇒ Q=∫_0 ^1 e^u sinu du IBP : { ((i=sinu)),((j′=e^u )) :} ⇒ { ((i′=cosu)),((j=e^u )) :} ⇒ Q = [e^u sinu]_0 ^1 −∫_0 ^1 e^u cosu du Double IBP : { ((i=cosu)),((j′=e^u )) :} ⇒ { ((i′=−sinu)),((j=e^u )) :} ⇒ Q= [e^u sinu−e^u cosu]_0 ^1 −∫_0 ^1 e^u sinu du ⇒ Q ={ (e^u /2)(sinu−cosu)}_0 ^1 ⇒ Q = {(e/2)(sin(1)−cos(1))}+(1/2) ∴∵ Q = (1/2){e(sin(1)−cos(1))+1}.. ..................Le puissant.................](https://www.tinkutara.com/question/Q156697.png)
$${Q}=\int_{\mathrm{0}} ^{\mathrm{1}} {sin}\left({lnx}\right){dx}\:;\:{u}={lnx}\rightarrow{x}={e}^{{u}} \rightarrow{dx}={e}^{{u}} {du} \\ $$$$\Rightarrow\:{Q}=\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{u}} {sinu}\:{du} \\ $$$${IBP}\::\:\begin{cases}{{i}={sinu}}\\{{j}'={e}^{{u}} }\end{cases}\:\:\Rightarrow\:\:\begin{cases}{{i}'={cosu}}\\{{j}={e}^{{u}} }\end{cases} \\ $$$$\Rightarrow\:{Q}\:=\:\left[{e}^{{u}} {sinu}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{u}} {cosu}\:{du} \\ $$$${Double}\:{IBP}\::\:\begin{cases}{{i}={cosu}}\\{{j}'={e}^{{u}} }\end{cases}\:\Rightarrow\:\begin{cases}{{i}'=−{sinu}}\\{{j}={e}^{{u}} }\end{cases} \\ $$$$\Rightarrow\:{Q}=\:\left[{e}^{{u}} {sinu}−{e}^{{u}} {cosu}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{u}} {sinu}\:{du} \\ $$$$\Rightarrow\:{Q}\:=\left\{\:\frac{{e}^{{u}} }{\mathrm{2}}\left({sinu}−{cosu}\right)\right\}_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\Rightarrow\:{Q}\:=\:\left\{\frac{{e}}{\mathrm{2}}\left({sin}\left(\mathrm{1}\right)−{cos}\left(\mathrm{1}\right)\right)\right\}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\therefore\because\:\:\:{Q}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left\{{e}\left({sin}\left(\mathrm{1}\right)−{cos}\left(\mathrm{1}\right)\right)+\mathrm{1}\right\}.. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:………………\mathscr{L}{e}\:{puissant}…………….. \\ $$
Commented by amin96 last updated on 14/Oct/21
$${very}\:{good}.\:{thanks}\:{sir}\: \\ $$
