Question Number 120461 by Khalmohmmad last updated on 31/Oct/20
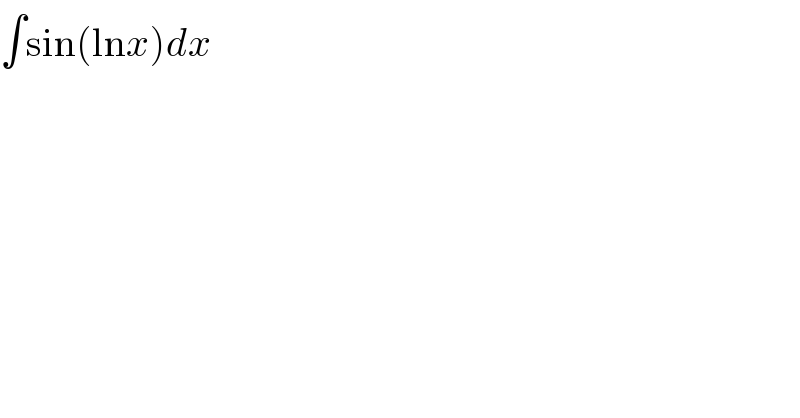
$$\int\mathrm{sin}\left(\mathrm{ln}{x}\right){dx} \\ $$
Answered by Dwaipayan Shikari last updated on 31/Oct/20
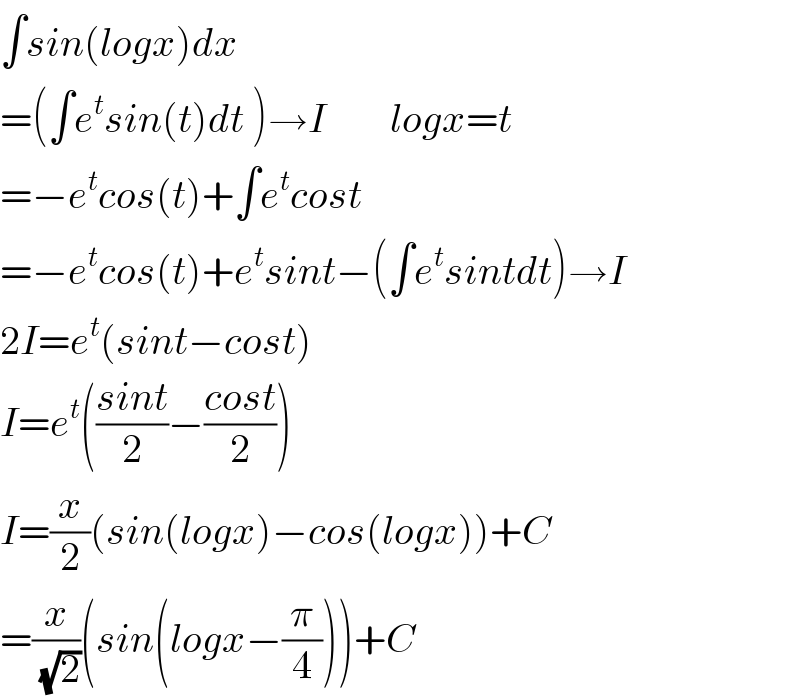
$$\int{sin}\left({logx}\right){dx} \\ $$$$=\left(\int{e}^{{t}} {sin}\left({t}\right){dt}\:\right)\rightarrow{I}\:\:\:\:\:\:\:\:{logx}={t} \\ $$$$=−{e}^{{t}} {cos}\left({t}\right)+\int{e}^{{t}} {cost} \\ $$$$=−{e}^{{t}} {cos}\left({t}\right)+{e}^{{t}} {sint}−\left(\int{e}^{{t}} {sintdt}\right)\rightarrow{I} \\ $$$$\mathrm{2}{I}={e}^{{t}} \left({sint}−{cost}\right) \\ $$$${I}={e}^{{t}} \left(\frac{{sint}}{\mathrm{2}}−\frac{{cost}}{\mathrm{2}}\right) \\ $$$${I}=\frac{{x}}{\mathrm{2}}\left({sin}\left({logx}\right)−{cos}\left({logx}\right)\right)+{C} \\ $$$$=\frac{{x}}{\:\sqrt{\mathrm{2}}}\left({sin}\left({logx}−\frac{\pi}{\mathrm{4}}\right)\right)+{C} \\ $$
