Question Number 158354 by cortano last updated on 03/Nov/21
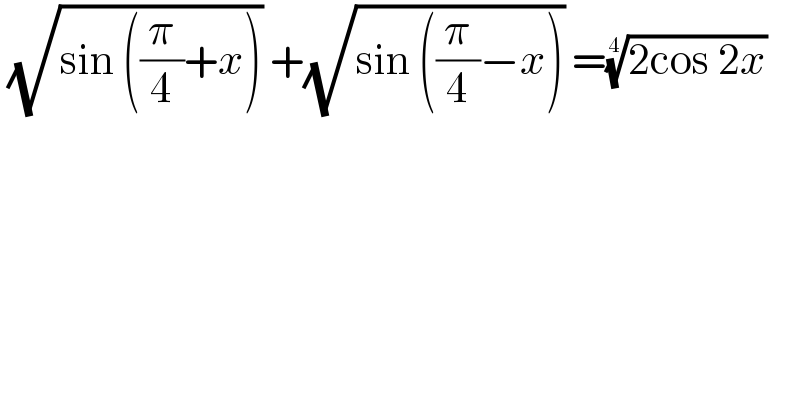
$$\:\sqrt{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}+{x}\right)}\:+\sqrt{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}−{x}\right)}\:=\sqrt[{\mathrm{4}}]{\mathrm{2cos}\:\mathrm{2}{x}} \\ $$
Commented by tounghoungko last updated on 03/Nov/21

$$\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}+{x}\right)+\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}−{x}\right)+\mathrm{2}\sqrt{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}+{x}\right)\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}−{x}\right)}=\sqrt{\mathrm{2cos}\:\mathrm{2}{x}} \\ $$$$\left({i}\right)\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}+{x}\right)+\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}−{x}\right)=\mathrm{2sin}\:\frac{\pi}{\mathrm{4}}\mathrm{cos}\:{x}=\sqrt{\mathrm{2}}\:\mathrm{cos}\:{x} \\ $$$$\left({ii}\right)\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}+{x}\right)\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}−{x}\right)=−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\:\frac{\pi}{\mathrm{2}}−\mathrm{cos}\:\mathrm{2}{x}\right)=\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}} \\ $$$$\Rightarrow\sqrt{\mathrm{2}}\mathrm{cos}\:{x}+\mathrm{2}\sqrt{\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}}}\:=\sqrt{\mathrm{2cos}\:\mathrm{2}{x}} \\ $$$$\Rightarrow\sqrt{\mathrm{2}}\:\mathrm{cos}\:{x}\:+\sqrt{\mathrm{2cos}\:\mathrm{2}{x}}\:=\:\sqrt{\mathrm{2cos}\:\mathrm{2}{x}} \\ $$$$\Rightarrow\mathrm{cos}\:{x}\:=\:\mathrm{0}\:\Rightarrow{x}=\frac{\pi}{\mathrm{2}} \\ $$$${check}\:{RHS}\:\Rightarrow\sqrt[{\mathrm{4}}]{\mathrm{2cos}\:\mathrm{2}{x}}\:=\sqrt[{\mathrm{4}}]{\mathrm{2cos}\:\pi}=\sqrt[{\mathrm{4}}]{−\mathrm{2}}\:\notin\mathbb{R} \\ $$$${so}\:{the}\:{equation}\:{has}\:{no}\:{solution} \\ $$
Commented by MJS_new last updated on 03/Nov/21
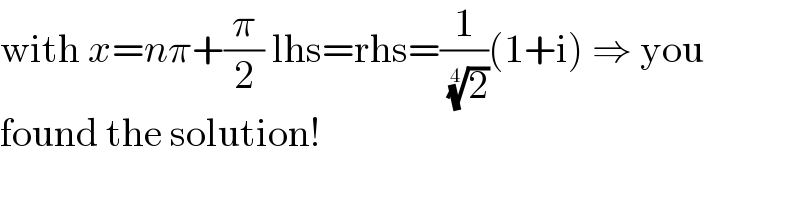
$$\mathrm{with}\:{x}={n}\pi+\frac{\pi}{\mathrm{2}}\:\mathrm{lhs}=\mathrm{rhs}=\frac{\mathrm{1}}{\:\sqrt[{\mathrm{4}}]{\mathrm{2}}}\left(\mathrm{1}+\mathrm{i}\right)\:\Rightarrow\:\mathrm{you} \\ $$$$\mathrm{found}\:\mathrm{the}\:\mathrm{solution}! \\ $$
