Question Number 183976 by cortano1 last updated on 01/Jan/23
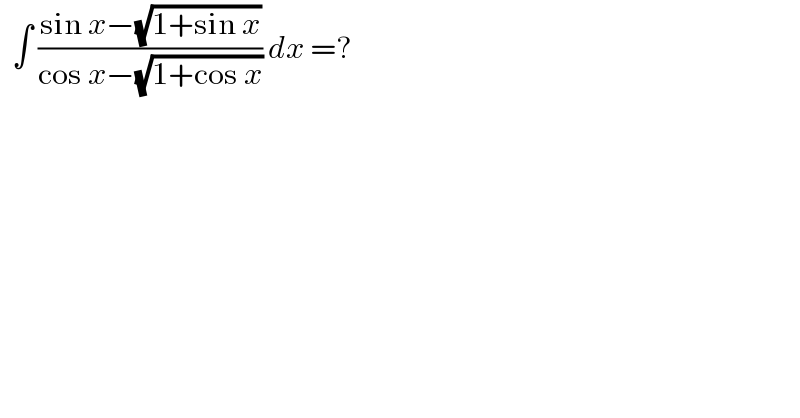
$$\:\:\int\:\frac{\mathrm{sin}\:{x}−\sqrt{\mathrm{1}+\mathrm{sin}\:{x}}}{\mathrm{cos}\:{x}−\sqrt{\mathrm{1}+\mathrm{cos}\:{x}}}\:{dx}\:=? \\ $$
Answered by MJS_new last updated on 01/Jan/23
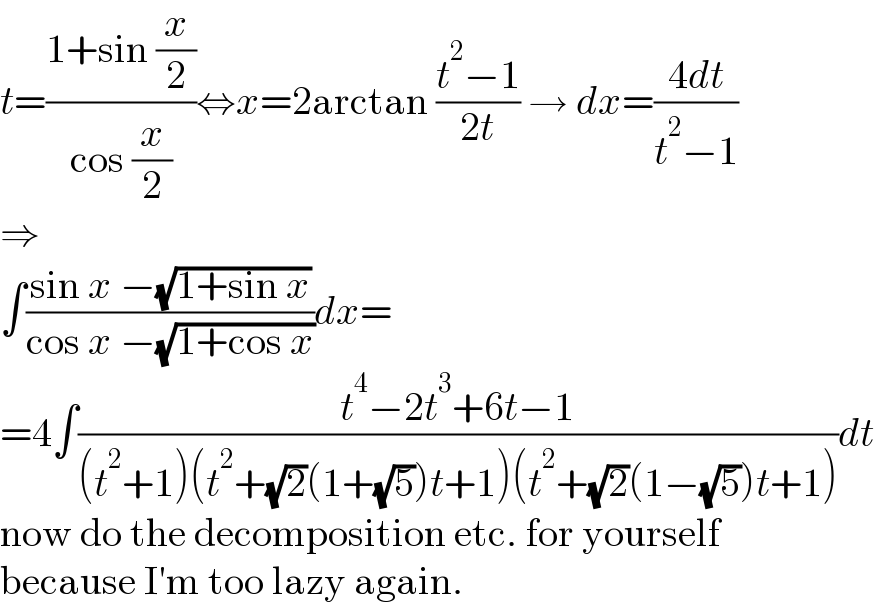
$${t}=\frac{\mathrm{1}+\mathrm{sin}\:\frac{{x}}{\mathrm{2}}}{\mathrm{cos}\:\frac{{x}}{\mathrm{2}}}\Leftrightarrow{x}=\mathrm{2arctan}\:\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{t}}\:\rightarrow\:{dx}=\frac{\mathrm{4}{dt}}{{t}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\Rightarrow \\ $$$$\int\frac{\mathrm{sin}\:{x}\:−\sqrt{\mathrm{1}+\mathrm{sin}\:{x}}}{\mathrm{cos}\:{x}\:−\sqrt{\mathrm{1}+\mathrm{cos}\:{x}}}{dx}= \\ $$$$=\mathrm{4}\int\frac{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{3}} +\mathrm{6}{t}−\mathrm{1}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} +\sqrt{\mathrm{2}}\left(\mathrm{1}+\sqrt{\mathrm{5}}\right){t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\sqrt{\mathrm{2}}\left(\mathrm{1}−\sqrt{\mathrm{5}}\right){t}+\mathrm{1}\right)}{dt} \\ $$$$\mathrm{now}\:\mathrm{do}\:\mathrm{the}\:\mathrm{decomposition}\:\mathrm{etc}.\:\mathrm{for}\:\mathrm{yourself} \\ $$$$\mathrm{because}\:\mathrm{I}'\mathrm{m}\:\mathrm{too}\:\mathrm{lazy}\:\mathrm{again}. \\ $$
