Question Number 145456 by math55 last updated on 05/Jul/21
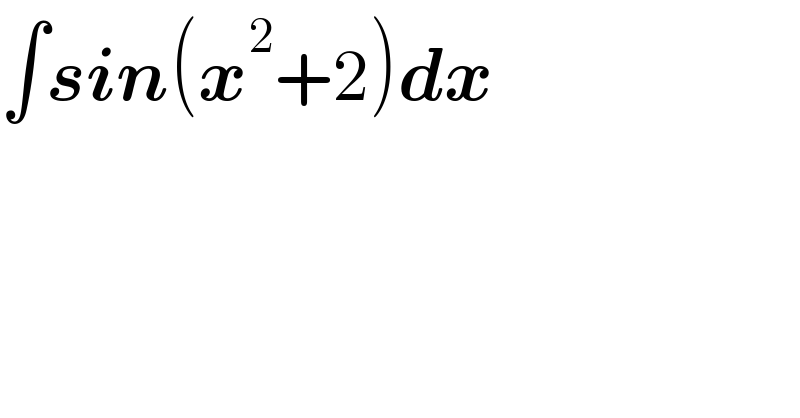
$$\int\boldsymbol{{sin}}\left(\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{2}\right)\boldsymbol{{dx}} \\ $$
Answered by Olaf_Thorendsen last updated on 05/Jul/21
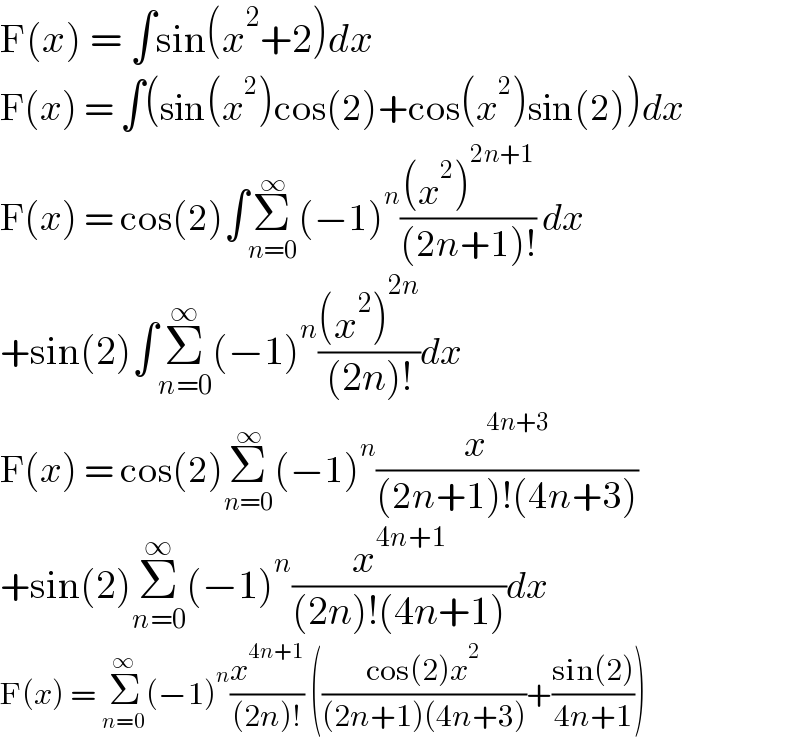
$$\mathrm{F}\left({x}\right)\:=\:\int\mathrm{sin}\left({x}^{\mathrm{2}} +\mathrm{2}\right){dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\int\left(\mathrm{sin}\left({x}^{\mathrm{2}} \right)\mathrm{cos}\left(\mathrm{2}\right)+\mathrm{cos}\left({x}^{\mathrm{2}} \right)\mathrm{sin}\left(\mathrm{2}\right)\right){dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{cos}\left(\mathrm{2}\right)\int\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{\left({x}^{\mathrm{2}} \right)^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:{dx} \\ $$$$+\mathrm{sin}\left(\mathrm{2}\right)\int\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{\left({x}^{\mathrm{2}} \right)^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{cos}\left(\mathrm{2}\right)\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{x}^{\mathrm{4}{n}+\mathrm{3}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!\left(\mathrm{4}{n}+\mathrm{3}\right)}\: \\ $$$$+\mathrm{sin}\left(\mathrm{2}\right)\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{x}^{\mathrm{4}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}\right)!\left(\mathrm{4}{n}+\mathrm{1}\right)}{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{x}^{\mathrm{4}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}\right)!}\:\left(\frac{\mathrm{cos}\left(\mathrm{2}\right){x}^{\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{4}{n}+\mathrm{3}\right)}+\frac{\mathrm{sin}\left(\mathrm{2}\right)}{\mathrm{4}{n}+\mathrm{1}}\right) \\ $$
