Menu Close

sin-x-2cos-x-3sin-x-4cos-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 123513 by bramlexs22 last updated on 26/Nov/20
∫ ((sin x+2cos x)/(3sin x+4cos x)) dx?
$$\int\:\frac{\mathrm{sin}\:{x}+\mathrm{2cos}\:{x}}{\mathrm{3sin}\:{x}+\mathrm{4cos}\:{x}}\:{dx}? \\ $$
Commented by liberty last updated on 26/Nov/20
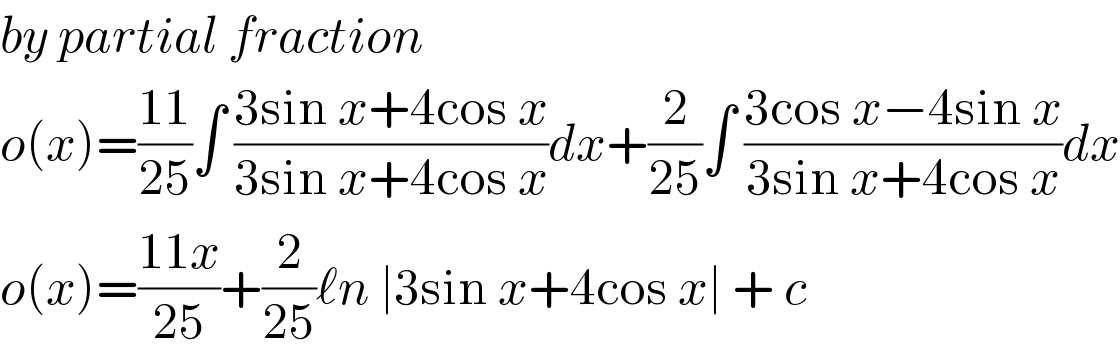
by partial fraction o(x)=((11)/(25))∫ ((3sin x+4cos x)/(3sin x+4cos x))dx+(2/(25))∫ ((3cos x−4sin x)/(3sin x+4cos x))dx o(x)=((11x)/(25))+(2/(25))ℓn ∣3sin x+4cos x∣ + c
$${by}\:{partial}\:{fraction} \\ $$$${o}\left({x}\right)=\frac{\mathrm{11}}{\mathrm{25}}\int\:\frac{\mathrm{3sin}\:{x}+\mathrm{4cos}\:{x}}{\mathrm{3sin}\:{x}+\mathrm{4cos}\:{x}}{dx}+\frac{\mathrm{2}}{\mathrm{25}}\int\:\frac{\mathrm{3cos}\:{x}−\mathrm{4sin}\:{x}}{\mathrm{3sin}\:{x}+\mathrm{4cos}\:{x}}{dx} \\ $$$${o}\left({x}\right)=\frac{\mathrm{11}{x}}{\mathrm{25}}+\frac{\mathrm{2}}{\mathrm{25}}\ell{n}\:\mid\mathrm{3sin}\:{x}+\mathrm{4cos}\:{x}\mid\:+\:{c}\: \\ $$
Answered by bramlexs22 last updated on 26/Nov/20
Answered by MJS_new last updated on 26/Nov/20
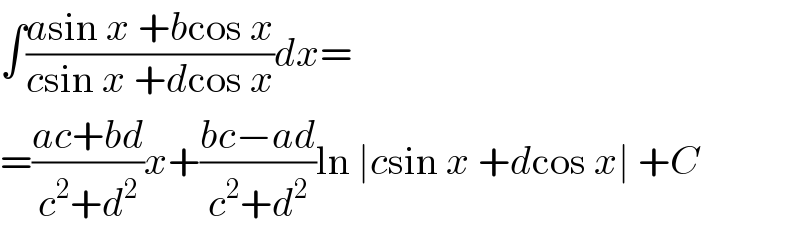
∫((asin x +bcos x)/(csin x +dcos x))dx= =((ac+bd)/(c^2 +d^2 ))x+((bc−ad)/(c^2 +d^2 ))ln ∣csin x +dcos x∣ +C
$$\int\frac{{a}\mathrm{sin}\:{x}\:+{b}\mathrm{cos}\:{x}}{{c}\mathrm{sin}\:{x}\:+{d}\mathrm{cos}\:{x}}{dx}= \\ $$$$=\frac{{ac}+{bd}}{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }{x}+\frac{{bc}−{ad}}{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }\mathrm{ln}\:\mid{c}\mathrm{sin}\:{x}\:+{d}\mathrm{cos}\:{x}\mid\:+{C} \\ $$
Commented by bramlexs22 last updated on 26/Nov/20
waw..superb sir
$${waw}..{superb}\:{sir} \\ $$
Answered by mathmax by abdo last updated on 26/Nov/20
I =∫ ((sinx+2cosx)/(3sinx+4cosx))dx we do the changement tan((x/2))=z ⇒ I =∫ ((((2z)/(1+z^2 ))+2((1−z^2 )/(1+z^2 )))/(3((2z)/(1+z^2 ))+4((1−z^2 )/(1+z^2 )))) ((2dz)/(1+z^2 )) =∫ ((2z+2−2z^2 )/((1+z^2 )(6z+4−4z^2 )))dz =∫ ((2z^2 −2z−2)/((z^2 +1)(4z^2 −6z−4)))dz =∫ ((z^2 −z−1)/((z^2 +1)(2z^2 −3z−2)))dz let decompose F(z) =((z^2 −z−1)/((z^2 +1)(2z^2 −3z−2))) 2z^2 −3z−2=0→Δ=9−4(2)(−2) =25 ⇒ z_1 =((3+5)/4)=2 and z_2 =((3−5)/4) =−(1/2) ⇒ F(z)=((z^2 −z−1)/((z−2)(z−(1/2))(z^2 +1))) =(a/(z−2))+(b/(z−(1/2))) +((cz +d)/(z^2 +1)) a =(1/((3/2)×5)) =(2/(15)) and b =(((1/4)−(3/2))/(((1/2)−2)((1/4)+1)))=−(5/4)×(1/((−(3/2))(5/4))) =(2/3) .... ⇒ ∫ F(z)dz =alog∣z−2∣+blog∣z−(1/2)∣+(c/2)ln(z^2 +1)+d arctanz +k= =a log∣tan((x/2))−2∣+blog∣tan((x/2))−(1/2)∣+(c/2)ln(1+tan^2 ((x/(2 )))) +(dx/2) +K
$$\mathrm{I}\:=\int\:\:\frac{\mathrm{sinx}+\mathrm{2cosx}}{\mathrm{3sinx}+\mathrm{4cosx}}\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{z}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\:\:\frac{\frac{\mathrm{2z}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }+\mathrm{2}\frac{\mathrm{1}−\mathrm{z}^{\mathrm{2}} }{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }}{\mathrm{3}\frac{\mathrm{2z}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }+\mathrm{4}\frac{\mathrm{1}−\mathrm{z}^{\mathrm{2}} }{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }}\:\frac{\mathrm{2dz}}{\mathrm{1}+\mathrm{z}^{\mathrm{2}} }\:=\int\:\:\:\frac{\mathrm{2z}+\mathrm{2}−\mathrm{2z}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)\left(\mathrm{6z}+\mathrm{4}−\mathrm{4z}^{\mathrm{2}} \right)}\mathrm{dz} \\ $$$$=\int\:\:\:\frac{\mathrm{2z}^{\mathrm{2}} −\mathrm{2z}−\mathrm{2}}{\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{4z}^{\mathrm{2}} −\mathrm{6z}−\mathrm{4}\right)}\mathrm{dz} \\ $$$$=\int\:\:\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{z}−\mathrm{1}}{\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{2z}^{\mathrm{2}} −\mathrm{3z}−\mathrm{2}\right)}\mathrm{dz}\:\:\mathrm{let}\:\mathrm{decompose} \\ $$$$\mathrm{F}\left(\mathrm{z}\right)\:=\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{z}−\mathrm{1}}{\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{2z}^{\mathrm{2}} −\mathrm{3z}−\mathrm{2}\right)} \\ $$$$\mathrm{2z}^{\mathrm{2}} −\mathrm{3z}−\mathrm{2}=\mathrm{0}\rightarrow\Delta=\mathrm{9}−\mathrm{4}\left(\mathrm{2}\right)\left(−\mathrm{2}\right)\:=\mathrm{25}\:\Rightarrow \\ $$$$\mathrm{z}_{\mathrm{1}} =\frac{\mathrm{3}+\mathrm{5}}{\mathrm{4}}=\mathrm{2}\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\frac{\mathrm{3}−\mathrm{5}}{\mathrm{4}}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{z}\right)=\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{z}−\mathrm{1}}{\left(\mathrm{z}−\mathrm{2}\right)\left(\mathrm{z}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\frac{\mathrm{a}}{\mathrm{z}−\mathrm{2}}+\frac{\mathrm{b}}{\mathrm{z}−\frac{\mathrm{1}}{\mathrm{2}}}\:+\frac{\mathrm{cz}\:+\mathrm{d}}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\mathrm{a}\:=\frac{\mathrm{1}}{\frac{\mathrm{3}}{\mathrm{2}}×\mathrm{5}}\:=\frac{\mathrm{2}}{\mathrm{15}}\:\:\mathrm{and}\:\mathrm{b}\:=\frac{\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{3}}{\mathrm{2}}}{\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}\right)\left(\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{1}\right)}=−\frac{\mathrm{5}}{\mathrm{4}}×\frac{\mathrm{1}}{\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)\frac{\mathrm{5}}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\:\:….\:\Rightarrow \\ $$$$\int\:\mathrm{F}\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{alog}\mid\mathrm{z}−\mathrm{2}\mid+\mathrm{blog}\mid\mathrm{z}−\frac{\mathrm{1}}{\mathrm{2}}\mid+\frac{\mathrm{c}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)+\mathrm{d}\:\mathrm{arctanz}\:+\mathrm{k}= \\ $$$$=\mathrm{a}\:\mathrm{log}\mid\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{2}\mid+\mathrm{blog}\mid\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mid+\frac{\mathrm{c}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}\:}\right)\right) \\ $$$$+\frac{\mathrm{dx}}{\mathrm{2}}\:+\mathrm{K} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *