Question Number 105904 by bemath last updated on 01/Aug/20
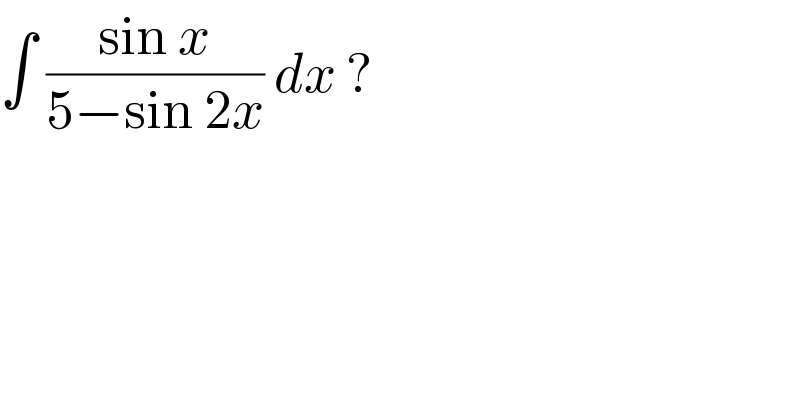
$$\int\:\frac{\mathrm{sin}\:{x}}{\mathrm{5}−\mathrm{sin}\:\mathrm{2}{x}}\:{dx}\:? \\ $$
Answered by bemath last updated on 01/Aug/20
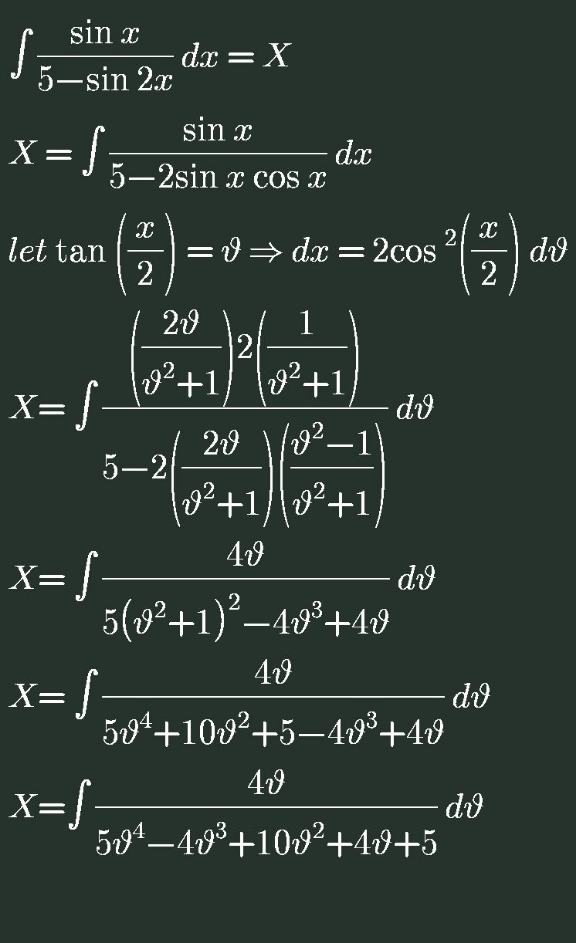
Commented by Her_Majesty last updated on 01/Aug/20
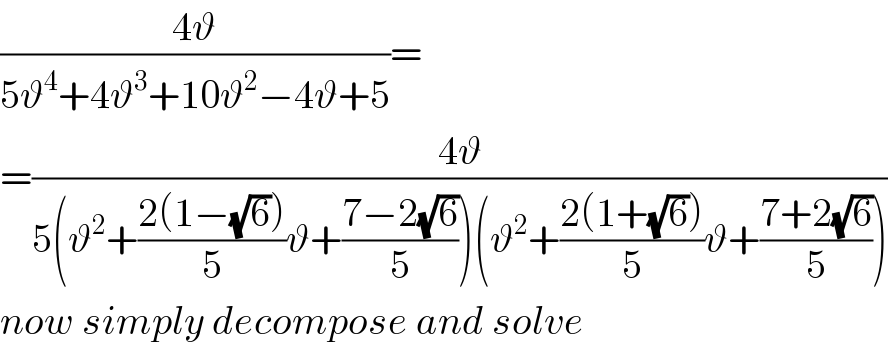
$$\frac{\mathrm{4}\vartheta}{\mathrm{5}\vartheta^{\mathrm{4}} +\mathrm{4}\vartheta^{\mathrm{3}} +\mathrm{10}\vartheta^{\mathrm{2}} −\mathrm{4}\vartheta+\mathrm{5}}= \\ $$$$=\frac{\mathrm{4}\vartheta}{\mathrm{5}\left(\vartheta^{\mathrm{2}} +\frac{\mathrm{2}\left(\mathrm{1}−\sqrt{\mathrm{6}}\right)}{\mathrm{5}}\vartheta+\frac{\mathrm{7}−\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{5}}\right)\left(\vartheta^{\mathrm{2}} +\frac{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{6}}\right)}{\mathrm{5}}\vartheta+\frac{\mathrm{7}+\mathrm{2}\sqrt{\mathrm{6}}}{\mathrm{5}}\right)} \\ $$$${now}\:{simply}\:{decompose}\:{and}\:{solve} \\ $$
Answered by 1549442205PVT last updated on 02/Aug/20

$$\mathrm{set}\:\mathrm{x}=\frac{\pi}{\mathrm{2}}−\mathrm{u}\:\Rightarrow\mathrm{dx}=−\mathrm{du},\mathrm{sinx}=\mathrm{sin}\left(\frac{\pi}{\mathrm{2}}−\mathrm{u}\right)=\mathrm{cosu} \\ $$$$\mathrm{sin2x}=\mathrm{sin2}\left(\frac{\pi}{\mathrm{2}}−\mathrm{u}\right)=\mathrm{sin}\left(\pi−\mathrm{2u}\right)=\mathrm{sin2u} \\ $$$$\Rightarrow\mathrm{F}=\int\:\frac{\mathrm{sinxdx}}{\mathrm{5}−\mathrm{sin2x}}=\int\frac{−\mathrm{cosu}}{\mathrm{5}−\mathrm{sin2u}}\mathrm{du} \\ $$$$\mathrm{Hence}\:\mathrm{2F}=\int\:\frac{\mathrm{sinxdx}}{\mathrm{5}−\mathrm{sin2x}}−\int\:\frac{\mathrm{cosxdx}}{\mathrm{5}−\mathrm{sin2x}} \\ $$$$=\int\:\frac{\mathrm{sinx}−\mathrm{cosx}}{\mathrm{5}−\mathrm{sin2x}}\mathrm{dx}=\int\:\frac{\mathrm{sinx}−\mathrm{cosx}}{\mathrm{4}+\left(\mathrm{1}−\mathrm{sin2x}\right)}\mathrm{dx} \\ $$$$=\int\:\frac{\left(\mathrm{sinx}−\mathrm{cosx}\right)\mathrm{dx}}{\mathrm{4}+\left(\mathrm{sinx}−\mathrm{cosx}\right)^{\mathrm{2}} }=\int\:\frac{\sqrt{\mathrm{2}}\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}−\mathrm{x}\right)\mathrm{dx}}{\mathrm{4}+\mathrm{2sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}−\mathrm{x}\right)} \\ $$$$\mathrm{Set}\:\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}−\mathrm{x}\right)=\mathrm{t}\Rightarrow\mathrm{dt}=\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}−\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{2F}=\int\:\frac{\sqrt{\mathrm{2}}\mathrm{dt}}{\mathrm{4}+\mathrm{2}\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)}=\int\:\frac{\sqrt{\mathrm{2}}\:\mathrm{dt}}{\mathrm{6}−\mathrm{2t}^{\mathrm{2}} }.\left(\mathrm{Since}\:\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2a}}\mathrm{ln}\mid\frac{\mathrm{x}−\mathrm{a}}{\mathrm{x}+\mathrm{a}}\mid\right) \\ $$$$=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}×\int\:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} −\left(\sqrt{\left.\mathrm{3}\right)^{\mathrm{2}} \:}\right.}=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{ln}\mid\frac{\mathrm{t}−\sqrt{\mathrm{3}}}{\mathrm{t}+\sqrt{\mathrm{3}}}\mid \\ $$$$\Rightarrow\boldsymbol{\mathrm{F}}=−\frac{\sqrt{\mathrm{2}}}{\mathrm{8}\sqrt{\mathrm{3}}}\boldsymbol{\mathrm{ln}}\mid\frac{\boldsymbol{\mathrm{t}}−\sqrt{\mathrm{3}}}{\boldsymbol{\mathrm{t}}+\sqrt{\mathrm{3}}}\mid=−\frac{\sqrt{\mathrm{2}}}{\mathrm{8}\sqrt{\mathrm{3}}}\boldsymbol{\mathrm{ln}}\mid\frac{\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}−\mathrm{x}\right)−\sqrt{\mathrm{3}}}{\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}−\mathrm{x}\right)+\sqrt{\mathrm{3}}}\mid \\ $$$$\boldsymbol{\mathrm{Please}},\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{friends}}\:\boldsymbol{\mathrm{check}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{help}}\:\:\boldsymbol{\mathrm{me}}. \\ $$$$\boldsymbol{\mathrm{Is}}\:\boldsymbol{\mathrm{it}}\:\boldsymbol{\mathrm{correct}}? \\ $$
Commented by bemath last updated on 02/Aug/20
$${cooll}…..{and}\:{great} \\ $$
Commented by Ar Brandon last updated on 02/Aug/20
![I think it would have been right in case we had integral limits. In that case x and u would have been considered as dummy variables. But here u remains a function in terms of x. ∫_a ^b f(x)dx=[F(x)]_a ^b =F(b)−F(a) ∫_a ^b f(u)du=[F(u)]_a ^b =F(b)−F(a) ⇒∫_a ^b f(x)dx=∫_a ^b f(u)du But without limits we′ll have; ∫f(x)dx=F(x)+C ∫f(u)du=F(u)+K F(x)+C≠F(u)+K](https://www.tinkutara.com/question/Q106126.png)
$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{would}\:\mathrm{have}\:\mathrm{been}\:\mathrm{right}\:\mathrm{in}\:\mathrm{case}\:\mathrm{we}\:\mathrm{had}\:\mathrm{integral} \\ $$$$\mathrm{limits}.\:\mathrm{In}\:\mathrm{that}\:\mathrm{case}\:\mathrm{x}\:\mathrm{and}\:\mathrm{u}\:\mathrm{would}\:\mathrm{have}\:\mathrm{been}\:\mathrm{considered} \\ $$$$\mathrm{as}\:\mathrm{dummy}\:\mathrm{variables}.\:\mathrm{But}\:\mathrm{here}\:\mathrm{u}\:\mathrm{remains}\:\mathrm{a}\:\mathrm{function}\:\mathrm{in}\:\mathrm{terms} \\ $$$$\mathrm{of}\:\mathrm{x}. \\ $$$$\int_{\mathrm{a}} ^{\mathrm{b}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\left[\mathrm{F}\left(\mathrm{x}\right)\right]_{\mathrm{a}} ^{\mathrm{b}} =\mathrm{F}\left(\mathrm{b}\right)−\mathrm{F}\left(\mathrm{a}\right) \\ $$$$\int_{\mathrm{a}} ^{\mathrm{b}} \mathrm{f}\left(\mathrm{u}\right)\mathrm{du}=\left[\mathrm{F}\left(\mathrm{u}\right)\right]_{\mathrm{a}} ^{\mathrm{b}} =\mathrm{F}\left(\mathrm{b}\right)−\mathrm{F}\left(\mathrm{a}\right) \\ $$$$\Rightarrow\int_{\mathrm{a}} ^{\mathrm{b}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\int_{\mathrm{a}} ^{\mathrm{b}} \mathrm{f}\left(\mathrm{u}\right)\mathrm{du} \\ $$$$\mathrm{But}\:\mathrm{without}\:\mathrm{limits}\:\mathrm{we}'\mathrm{ll}\:\mathrm{have}; \\ $$$$\int\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\mathrm{F}\left(\mathrm{x}\right)+\mathrm{C} \\ $$$$\int\mathrm{f}\left(\mathrm{u}\right)\mathrm{du}=\mathrm{F}\left(\mathrm{u}\right)+\mathrm{K} \\ $$$$\mathrm{F}\left(\mathrm{x}\right)+\mathrm{C}\neq\mathrm{F}\left(\mathrm{u}\right)+\mathrm{K} \\ $$
