Question Number 85383 by M±th+et£s last updated on 21/Mar/20
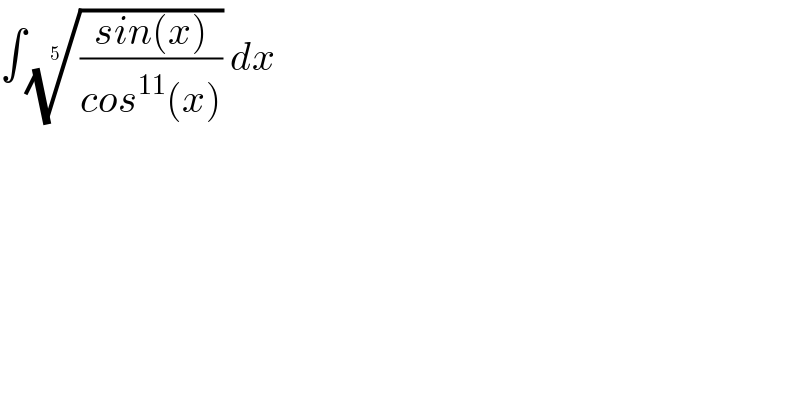
$$\int\sqrt[{\mathrm{5}}]{\frac{{sin}\left({x}\right)}{{cos}^{\mathrm{11}} \left({x}\right)}}\:{dx} \\ $$
Answered by john santu last updated on 21/Mar/20
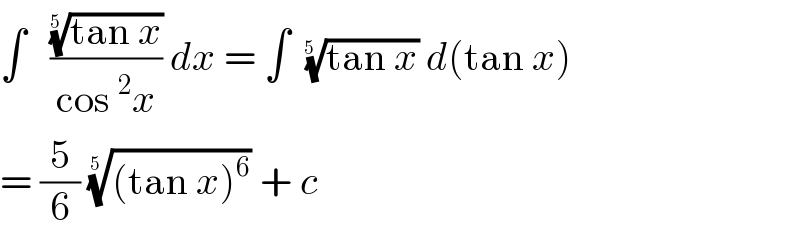
$$\int\:\:\:\frac{\sqrt[{\mathrm{5}\:}]{\mathrm{tan}\:{x}}}{\mathrm{cos}\:^{\mathrm{2}} {x}}\:{dx}\:=\:\int\:\:\sqrt[{\mathrm{5}\:\:}]{\mathrm{tan}\:{x}}\:{d}\left(\mathrm{tan}\:{x}\right) \\ $$$$=\:\frac{\mathrm{5}}{\mathrm{6}}\:\sqrt[{\mathrm{5}\:\:}]{\left(\mathrm{tan}\:{x}\right)^{\mathrm{6}} }\:+\:{c} \\ $$
Commented by M±th+et£s last updated on 21/Mar/20

$${thank}\:{you}\:{sir} \\ $$
