Question Number 85718 by M±th+et£s last updated on 24/Mar/20
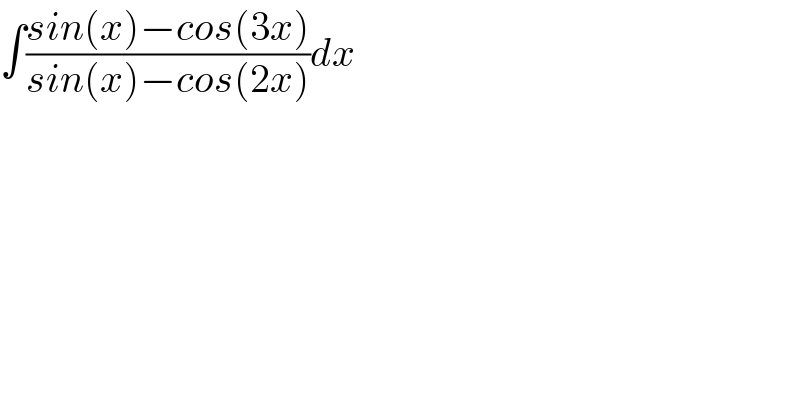
$$\int\frac{{sin}\left({x}\right)−{cos}\left(\mathrm{3}{x}\right)}{{sin}\left({x}\right)−{cos}\left(\mathrm{2}{x}\right)}{dx} \\ $$
Answered by MJS last updated on 24/Mar/20
![∫((sin x −cos 3x)/(sin x −cos 2x))dx= =∫((4cos x sin^2 x −cos x +sin x)/(−2cos^2 x +sin x +1))dx= [t=tan (x/2) → dx=((2dt)/(t^2 +1))] =−2∫((t^6 +2t^5 −15t^4 +4t^3 +15t^2 +2t−1)/(t^8 −2t^7 −4t^6 −6t^5 −10t^4 −6t^3 −4t^2 −2t+1))dt= =−2∫((...)/((t^2 +1)^2 (t+1)^2 (t−2−(√3))(t−2+(√3))))dt= =8∫(dt/((t^2 +1)^2 ))+∫((2t)/(t^2 +1))dt−4∫(dt/(t^2 +1))+(2/3)∫(dt/((t^2 +1)^2 ))−2∫(dt/(t+1))−((√3)/9)∫(dt/(t−2−(√3)))+((√3)/9)∫(dt/(t−2+(√3))) now it′s easy](https://www.tinkutara.com/question/Q85754.png)
$$\int\frac{\mathrm{sin}\:{x}\:−\mathrm{cos}\:\mathrm{3}{x}}{\mathrm{sin}\:{x}\:−\mathrm{cos}\:\mathrm{2}{x}}{dx}= \\ $$$$=\int\frac{\mathrm{4cos}\:{x}\:\mathrm{sin}^{\mathrm{2}} \:{x}\:−\mathrm{cos}\:{x}\:+\mathrm{sin}\:{x}}{−\mathrm{2cos}^{\mathrm{2}} \:{x}\:+\mathrm{sin}\:{x}\:+\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=−\mathrm{2}\int\frac{{t}^{\mathrm{6}} +\mathrm{2}{t}^{\mathrm{5}} −\mathrm{15}{t}^{\mathrm{4}} +\mathrm{4}{t}^{\mathrm{3}} +\mathrm{15}{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}}{{t}^{\mathrm{8}} −\mathrm{2}{t}^{\mathrm{7}} −\mathrm{4}{t}^{\mathrm{6}} −\mathrm{6}{t}^{\mathrm{5}} −\mathrm{10}{t}^{\mathrm{4}} −\mathrm{6}{t}^{\mathrm{3}} −\mathrm{4}{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}}{dt}= \\ $$$$=−\mathrm{2}\int\frac{…}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left({t}+\mathrm{1}\right)^{\mathrm{2}} \left({t}−\mathrm{2}−\sqrt{\mathrm{3}}\right)\left({t}−\mathrm{2}+\sqrt{\mathrm{3}}\right)}{dt}= \\ $$$$=\mathrm{8}\int\frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\int\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}−\mathrm{4}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }−\mathrm{2}\int\frac{{dt}}{{t}+\mathrm{1}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{9}}\int\frac{{dt}}{{t}−\mathrm{2}−\sqrt{\mathrm{3}}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{9}}\int\frac{{dt}}{{t}−\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$$\mathrm{now}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy} \\ $$
Commented by MJS last updated on 24/Mar/20
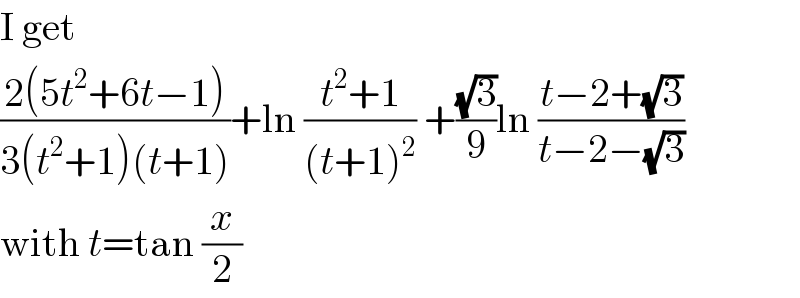
$$\mathrm{I}\:\mathrm{get} \\ $$$$\frac{\mathrm{2}\left(\mathrm{5}{t}^{\mathrm{2}} +\mathrm{6}{t}−\mathrm{1}\right)}{\mathrm{3}\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}+\mathrm{1}\right)}+\mathrm{ln}\:\frac{{t}^{\mathrm{2}} +\mathrm{1}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{ln}\:\frac{{t}−\mathrm{2}+\sqrt{\mathrm{3}}}{{t}−\mathrm{2}−\sqrt{\mathrm{3}}} \\ $$$$\mathrm{with}\:{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}} \\ $$
Commented by M±th+et£s last updated on 24/Mar/20

$${thank}\:{you}\:{sir}\:.\:{god}\:{bless}\:{you} \\ $$
