Question Number 124043 by liberty last updated on 30/Nov/20
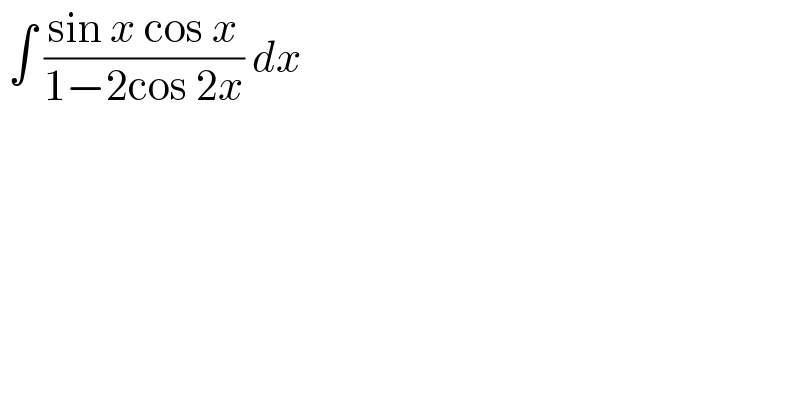
$$\:\int\:\frac{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}{\mathrm{1}−\mathrm{2cos}\:\mathrm{2}{x}}\:{dx}\: \\ $$
Answered by john_santu last updated on 30/Nov/20
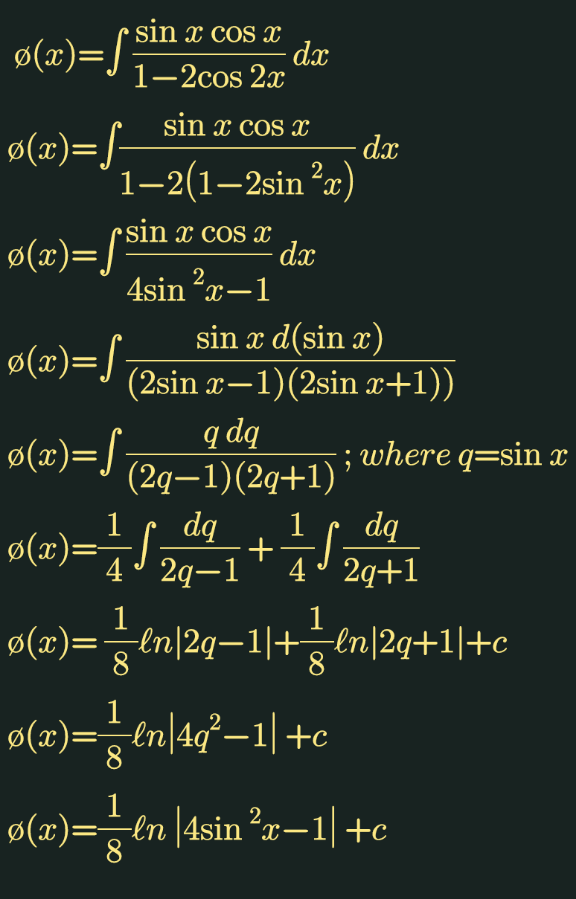
Answered by Dwaipayan Shikari last updated on 30/Nov/20
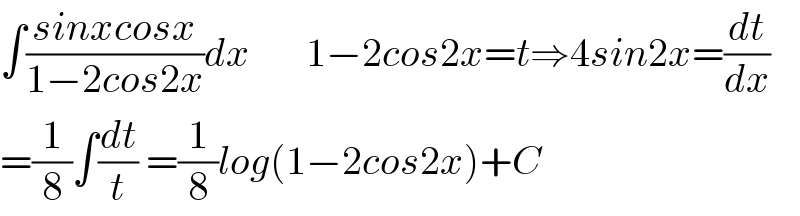
$$\int\frac{{sinxcosx}}{\mathrm{1}−\mathrm{2}{cos}\mathrm{2}{x}}{dx}\:\:\:\:\:\:\:\mathrm{1}−\mathrm{2}{cos}\mathrm{2}{x}={t}\Rightarrow\mathrm{4}{sin}\mathrm{2}{x}=\frac{{dt}}{{dx}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int\frac{{dt}}{{t}}\:=\frac{\mathrm{1}}{\mathrm{8}}{log}\left(\mathrm{1}−\mathrm{2}{cos}\mathrm{2}{x}\right)+{C} \\ $$
