Menu Close

sin-x-cos-x-3sin-x-4cos-x-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 126753 by bemath last updated on 24/Dec/20
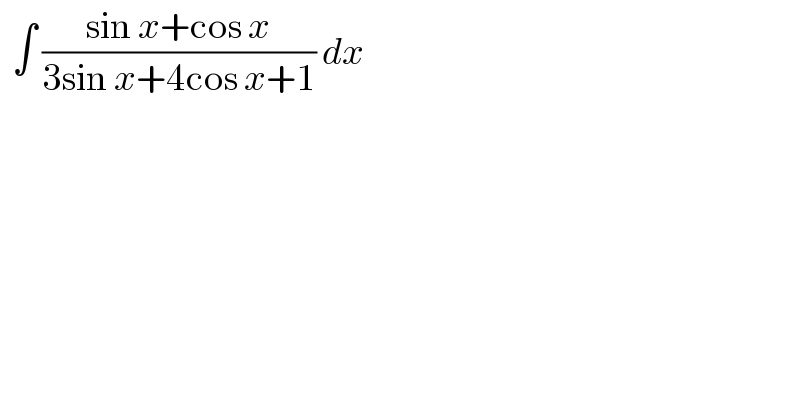
∫ ((sin x+cos x)/(3sin x+4cos x+1)) dx
$$\:\:\int\:\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\mathrm{3sin}\:{x}+\mathrm{4cos}\:{x}+\mathrm{1}}\:{dx}\: \\ $$
Answered by Ar Brandon last updated on 24/Dec/20
sinx+cosx=λ(3sinx+4cosx+1)+μ{(d/dx)(3sinx+4cosx+1)}+γ =λ(3sinx+4cosx+1)+μ(3cosx−4sinx)+γ { ((3λ−4μ=1)),((4λ+3μ=1)),((λ+γ=0)) :}⇒ { ((25μ=−1)),((25λ=7)),((γ=−λ)) :} I=∫((sinx+cosx)/(3sinx+4cosx+1))dx =(7/(25))∫((3sinx+4cosx+1)/(3sinx+4cosx+1))dx−(1/(25))∫((3cosx−4sinx)/(3sinx+4cosx+1))dx −(7/(25))∫(dx/(3sinx+4cosx+1)) =(7/(25))x−(1/(25))ln∣3sinx+4cosx+1∣−(7/(25))J tan(x/2)=t ⇒ sec^2 (x/2)dx=2tdt ⇒ dx=((2t)/(t^2 +1))dt J=∫(1/(((3t)/(t^2 +1))−4((t^2 −1)/(t^2 +1))+1))∙((2t)/(t^2 +1))dt=∫((2t)/(3t−4(t^2 −1)+(t^2 +1)))dt =∫((2t)/(−3t^2 +3t+5))dt=−∫((2t)/(3t^2 −3t−5))dt 2t=μ{(d/dt)(3t^2 −3t−5)}+γ=μ(6t−3)+γ { ((6μ=2)),((γ−3μ=0)) :} ⇒ { ((μ=(1/3))),((γ=1)) :} J=−∫{(1/3)∙((6t−3)/(3t^2 −3t−5))+(1/(3t^2 −3t−5))}dt =−{(1/3)ln∣3t^2 −3t−5∣−((2(√3))/( 3(√(23))))Arctanh((2t−1)(√(3/(23))))}+C =−((ln∣3t^2 −3t−5∣)/3)+(1/( (√(69))))ln∣((2t−1+3/(√(69)))/(2t−1−3/(√(69))))∣+C I=(7/(25))x−((ln∣3sinx+4cosx+1∣)/(25))+(7/(75))ln∣3tan^2 ((x/2))−3tan((x/2))−5∣ −(7/( 25(√(69))))ln∣((2tan(x/2)−1+3/(√(69)))/(2tan(x/2)−1−3/(√(69))))∣+C
$$\mathrm{sinx}+\mathrm{cosx}=\lambda\left(\mathrm{3sinx}+\mathrm{4cosx}+\mathrm{1}\right)+\mu\left\{\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{3sinx}+\mathrm{4cosx}+\mathrm{1}\right)\right\}+\gamma \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\lambda\left(\mathrm{3sinx}+\mathrm{4cosx}+\mathrm{1}\right)+\mu\left(\mathrm{3cosx}−\mathrm{4sinx}\right)+\gamma \\ $$$$\begin{cases}{\mathrm{3}\lambda−\mathrm{4}\mu=\mathrm{1}}\\{\mathrm{4}\lambda+\mathrm{3}\mu=\mathrm{1}}\\{\lambda+\gamma=\mathrm{0}}\end{cases}\Rightarrow\begin{cases}{\mathrm{25}\mu=−\mathrm{1}}\\{\mathrm{25}\lambda=\mathrm{7}}\\{\gamma=−\lambda}\end{cases} \\ $$$$\mathcal{I}=\int\frac{\mathrm{sinx}+\mathrm{cosx}}{\mathrm{3sinx}+\mathrm{4cosx}+\mathrm{1}}\mathrm{dx} \\ $$$$\:\:\:=\frac{\mathrm{7}}{\mathrm{25}}\int\frac{\mathrm{3sinx}+\mathrm{4cosx}+\mathrm{1}}{\mathrm{3sinx}+\mathrm{4cosx}+\mathrm{1}}\mathrm{dx}−\frac{\mathrm{1}}{\mathrm{25}}\int\frac{\mathrm{3cosx}−\mathrm{4sinx}}{\mathrm{3sinx}+\mathrm{4cosx}+\mathrm{1}}\mathrm{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{7}}{\mathrm{25}}\int\frac{\mathrm{dx}}{\mathrm{3sinx}+\mathrm{4cosx}+\mathrm{1}} \\ $$$$\:\:\:=\frac{\mathrm{7}}{\mathrm{25}}\mathrm{x}−\frac{\mathrm{1}}{\mathrm{25}}\mathrm{ln}\mid\mathrm{3sinx}+\mathrm{4cosx}+\mathrm{1}\mid−\frac{\mathrm{7}}{\mathrm{25}}\mathcal{J} \\ $$$$\mathrm{tan}\frac{\mathrm{x}}{\mathrm{2}}=\mathrm{t}\:\Rightarrow\:\mathrm{sec}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}\mathrm{dx}=\mathrm{2tdt}\:\Rightarrow\:\mathrm{dx}=\frac{\mathrm{2t}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}\mathrm{dt} \\ $$$$\mathcal{J}=\int\frac{\mathrm{1}}{\frac{\mathrm{3t}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}−\mathrm{4}\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}+\mathrm{1}}\centerdot\frac{\mathrm{2t}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}\mathrm{dt}=\int\frac{\mathrm{2t}}{\mathrm{3t}−\mathrm{4}\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)+\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}\mathrm{dt} \\ $$$$\:\:\:\:=\int\frac{\mathrm{2t}}{−\mathrm{3t}^{\mathrm{2}} +\mathrm{3t}+\mathrm{5}}\mathrm{dt}=−\int\frac{\mathrm{2t}}{\mathrm{3t}^{\mathrm{2}} −\mathrm{3t}−\mathrm{5}}\mathrm{dt} \\ $$$$\mathrm{2t}=\mu\left\{\frac{\mathrm{d}}{\mathrm{dt}}\left(\mathrm{3t}^{\mathrm{2}} −\mathrm{3t}−\mathrm{5}\right)\right\}+\gamma=\mu\left(\mathrm{6t}−\mathrm{3}\right)+\gamma \\ $$$$\begin{cases}{\mathrm{6}\mu=\mathrm{2}}\\{\gamma−\mathrm{3}\mu=\mathrm{0}}\end{cases}\:\Rightarrow\begin{cases}{\mu=\frac{\mathrm{1}}{\mathrm{3}}}\\{\gamma=\mathrm{1}}\end{cases} \\ $$$$\mathcal{J}=−\int\left\{\frac{\mathrm{1}}{\mathrm{3}}\centerdot\frac{\mathrm{6t}−\mathrm{3}}{\mathrm{3t}^{\mathrm{2}} −\mathrm{3t}−\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{3t}^{\mathrm{2}} −\mathrm{3t}−\mathrm{5}}\right\}\mathrm{dt} \\ $$$$\:\:\:\:=−\left\{\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\mid\mathrm{3t}^{\mathrm{2}} −\mathrm{3t}−\mathrm{5}\mid−\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\:\mathrm{3}\sqrt{\mathrm{23}}}\mathrm{Arctanh}\left(\left(\mathrm{2t}−\mathrm{1}\right)\sqrt{\frac{\mathrm{3}}{\mathrm{23}}}\right)\right\}+\mathcal{C} \\ $$$$\:\:\:\:=−\frac{\mathrm{ln}\mid\mathrm{3t}^{\mathrm{2}} −\mathrm{3t}−\mathrm{5}\mid}{\mathrm{3}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{69}}}\mathrm{ln}\mid\frac{\mathrm{2t}−\mathrm{1}+\mathrm{3}/\sqrt{\mathrm{69}}}{\mathrm{2t}−\mathrm{1}−\mathrm{3}/\sqrt{\mathrm{69}}}\mid+\mathcal{C} \\ $$$$\mathcal{I}=\frac{\mathrm{7}}{\mathrm{25}}\mathrm{x}−\frac{\mathrm{ln}\mid\mathrm{3sinx}+\mathrm{4cosx}+\mathrm{1}\mid}{\mathrm{25}}+\frac{\mathrm{7}}{\mathrm{75}}\mathrm{ln}\mid\mathrm{3tan}^{\mathrm{2}} \left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{3tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)−\mathrm{5}\mid \\ $$$$\:\:\:\:\:\:\:−\frac{\mathrm{7}}{\:\mathrm{25}\sqrt{\mathrm{69}}}\mathrm{ln}\mid\frac{\mathrm{2tan}\left(\mathrm{x}/\mathrm{2}\right)−\mathrm{1}+\mathrm{3}/\sqrt{\mathrm{69}}}{\mathrm{2tan}\left(\mathrm{x}/\mathrm{2}\right)−\mathrm{1}−\mathrm{3}/\sqrt{\mathrm{69}}}\mid+\mathcal{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *