Question Number 52893 by dwdkswd last updated on 14/Jan/19
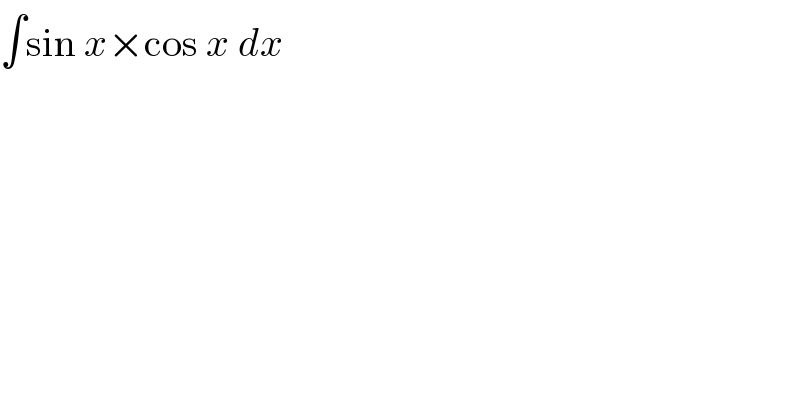
$$\int\mathrm{sin}\:{x}×\mathrm{cos}\:{x}\:{dx} \\ $$
Answered by MJS last updated on 14/Jan/19
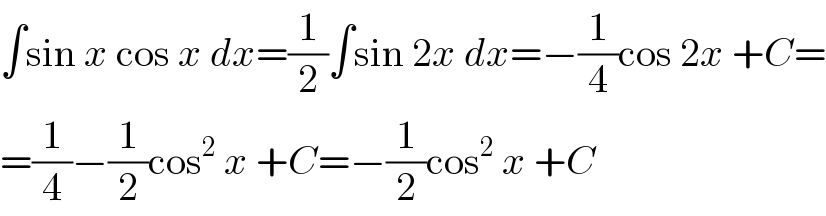
$$\int\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}\:{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{sin}\:\mathrm{2}{x}\:{dx}=−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\:\mathrm{2}{x}\:+{C}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{\mathrm{2}} \:{x}\:+{C}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{\mathrm{2}} \:{x}\:+{C} \\ $$
