Question Number 116501 by bemath last updated on 04/Oct/20
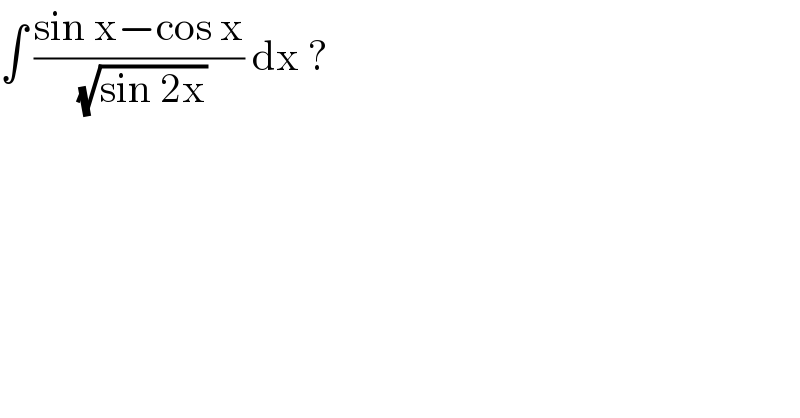
$$\int\:\frac{\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}}{\:\sqrt{\mathrm{sin}\:\mathrm{2x}}}\:\mathrm{dx}\:? \\ $$
Answered by TANMAY PANACEA last updated on 04/Oct/20
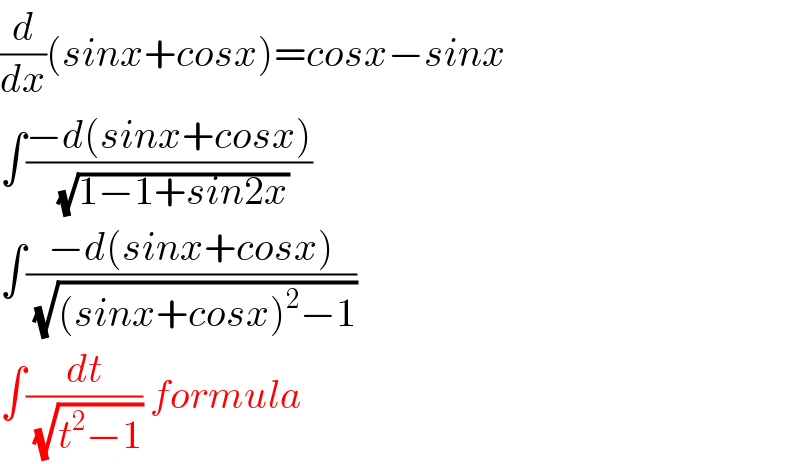
$$\frac{{d}}{{dx}}\left({sinx}+{cosx}\right)={cosx}−{sinx} \\ $$$$\int\frac{−{d}\left({sinx}+{cosx}\right)}{\:\sqrt{\mathrm{1}−\mathrm{1}+{sin}\mathrm{2}{x}}} \\ $$$$\int\frac{−{d}\left({sinx}+{cosx}\right)}{\:\sqrt{\left({sinx}+{cosx}\right)^{\mathrm{2}} −\mathrm{1}}} \\ $$$$\int\frac{{dt}}{\:\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}\:{formula} \\ $$
Commented by bemath last updated on 04/Oct/20
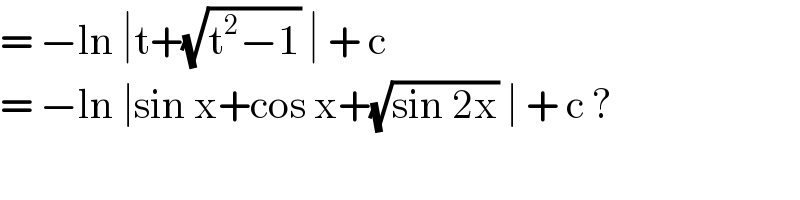
$$=\:−\mathrm{ln}\:\mid\mathrm{t}+\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\:\mid\:+\:\mathrm{c}\: \\ $$$$=\:−\mathrm{ln}\:\mid\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}+\sqrt{\mathrm{sin}\:\mathrm{2x}}\:\mid\:+\:\mathrm{c}\:? \\ $$
Commented by MJS_new last updated on 04/Oct/20

$$\mathrm{yes} \\ $$
