Menu Close

sin-x-cos-x-sin-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 126586 by benjo_mathlover last updated on 22/Dec/20
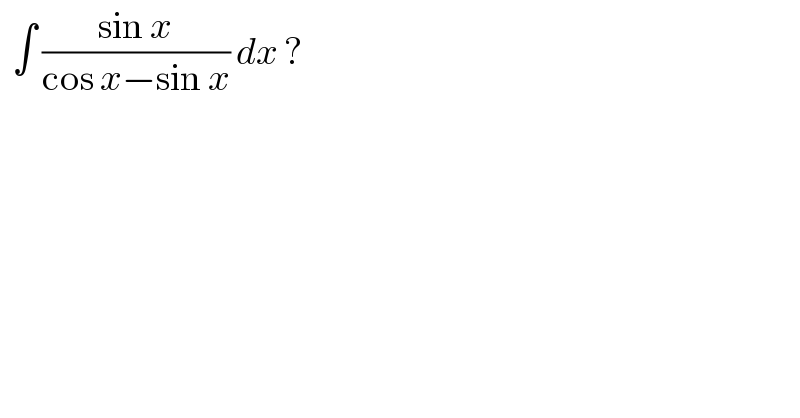
∫ ((sin x)/(cos x−sin x)) dx ?
$$\:\:\int\:\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}\:{dx}\:? \\ $$
Answered by liberty last updated on 22/Dec/20
partial fraction ((sin x)/(cos x−sin x)) = P(((cos x−sin x)/(cos x−sin x)))+Q (((d/dx)(cos x−sin x))/(cos x−sin x)) ⇔ sin x = P(cos x−sin x)+Q(−sin x−cos x) ⇔ sin x = (−P−Q)sin x+(P−Q)cos x → { ((P−Q=0)),((−P−Q=1→ { ((P=−(1/2))),((Q=−(1/2))) :})) :} then ∫((sin x)/(cos x−sin x))dx = −(1/2)∫ dx−(1/2)∫((d(cos x−sin x))/(cos x−sin x)) = −(1/2)x−(1/2)ℓn ∣cos x−sin x∣ + c
$${partial}\:{fraction} \\ $$$$\:\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}\:=\:{P}\left(\frac{\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}\right)+{Q}\:\frac{\frac{{d}}{{dx}}\left(\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right)}{\mathrm{cos}\:{x}−\mathrm{sin}\:{x}} \\ $$$$\Leftrightarrow\:\mathrm{sin}\:{x}\:=\:{P}\left(\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right)+{Q}\left(−\mathrm{sin}\:{x}−\mathrm{cos}\:{x}\right) \\ $$$$\Leftrightarrow\:\mathrm{sin}\:{x}\:=\:\left(−{P}−{Q}\right)\mathrm{sin}\:{x}+\left({P}−{Q}\right)\mathrm{cos}\:{x} \\ $$$$\:\rightarrow\begin{cases}{{P}−{Q}=\mathrm{0}}\\{−{P}−{Q}=\mathrm{1}\rightarrow\begin{cases}{{P}=−\frac{\mathrm{1}}{\mathrm{2}}}\\{{Q}=−\frac{\mathrm{1}}{\mathrm{2}}}\end{cases}}\end{cases} \\ $$$${then}\:\int\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}{dx}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\int\:{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left(\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right)}{\mathrm{cos}\:{x}−\mathrm{sin}\:{x}} \\ $$$$\:=\:−\frac{\mathrm{1}}{\mathrm{2}}{x}−\frac{\mathrm{1}}{\mathrm{2}}\ell{n}\:\mid\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\mid\:+\:{c}\: \\ $$
Answered by Ar Brandon last updated on 22/Dec/20
sinx=λ(cosx−sinx)+μ{(d/dx)(cosx−sinx)} =λ(cosx−sinx)+μ(−sinx−cosx) λ−μ=0, −λ−μ=1 ⇒ λ=−(1/2)=μ I=−(1/2)∫{((cosx−sinx)/(cosx−sinx))+((−sinx−cosx)/(cosx−sinx))}dx =−(1/2){x+ln∣cosx−sinx∣}+C
$$\mathrm{sinx}=\lambda\left(\mathrm{cosx}−\mathrm{sinx}\right)+\mu\left\{\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{cosx}−\mathrm{sinx}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\lambda\left(\mathrm{cosx}−\mathrm{sinx}\right)+\mu\left(−\mathrm{sinx}−\mathrm{cosx}\right) \\ $$$$\lambda−\mu=\mathrm{0},\:−\lambda−\mu=\mathrm{1}\:\Rightarrow\:\lambda=−\frac{\mathrm{1}}{\mathrm{2}}=\mu \\ $$$$\mathcal{I}=−\frac{\mathrm{1}}{\mathrm{2}}\int\left\{\frac{\mathrm{cosx}−\mathrm{sinx}}{\mathrm{cosx}−\mathrm{sinx}}+\frac{−\mathrm{sinx}−\mathrm{cosx}}{\mathrm{cosx}−\mathrm{sinx}}\right\}\mathrm{dx} \\ $$$$\:\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{x}+\mathrm{ln}\mid\mathrm{cosx}−\mathrm{sinx}\mid\right\}+\mathrm{C} \\ $$
Answered by chengulapetrom last updated on 22/Dec/20
=(1/2)∫((2sinx)/(cosx−sinx))dx =(1/2)∫((sinx−cosx+sinx+cosx)/(cosx−sinx))dx =−(1/2)∫((cosx−sinx)/(cosx−sinx))dx+(1/2)∫((sinx+cosx)/(cosx−sinx))dx =−(1/2)x−(1/2)ln∣cosx−sinx∣+C any suggestion
$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{sinx}}{{cosx}−{sinx}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{sinx}−{cosx}+{sinx}+{cosx}}{{cosx}−{sinx}}{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{cosx}−{sinx}}{{cosx}−{sinx}}{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{sinx}+{cosx}}{{cosx}−{sinx}}{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{x}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{cosx}−{sinx}\mid+{C} \\ $$$${any}\:{suggestion} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *