Question Number 183279 by cortano1 last updated on 24/Dec/22
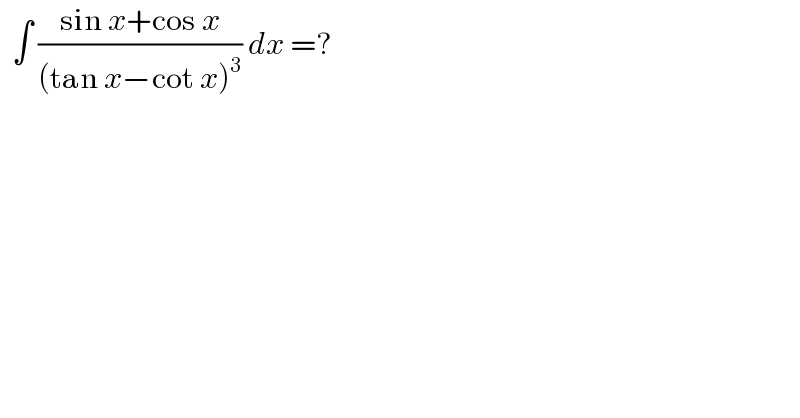
$$\:\:\int\:\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\left(\mathrm{tan}\:{x}−\mathrm{cot}\:{x}\right)^{\mathrm{3}} }\:{dx}\:=? \\ $$
Answered by MJS_new last updated on 24/Dec/22
![with t=tan (x/2) we get −16∫((t^3 (t^2 −1)^3 )/((t^2 +1)^2 (t^2 −2t−1)^2 (t^2 +2t−1)^3 ))dt= [Ostrogradski′s Method] =−(((t+1)(9t^6 −57t^4 −104t^3 +51t^2 +24t−11))/(32(t^2 +1)(t^2 −2t−1)(t^2 +2t−1)^2 ))−(9/(32))∫(dt/(t^2 +2t−1))= =−(((t+1)(9t^6 −57t^4 −104t^3 +51t^2 +24t−11))/(32(t^2 +1)(t^2 −2t−1)(t^2 +2t−1)^2 ))+((9(√2))/(128))ln ((t+1+(√2))/(t+1−(√2))) ...](https://www.tinkutara.com/question/Q183289.png)
$$\mathrm{with}\:{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\mathrm{we}\:\mathrm{get} \\ $$$$−\mathrm{16}\int\frac{{t}^{\mathrm{3}} \left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{2}} \left({t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{3}} }{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=−\frac{\left({t}+\mathrm{1}\right)\left(\mathrm{9}{t}^{\mathrm{6}} −\mathrm{57}{t}^{\mathrm{4}} −\mathrm{104}{t}^{\mathrm{3}} +\mathrm{51}{t}^{\mathrm{2}} +\mathrm{24}{t}−\mathrm{11}\right)}{\mathrm{32}\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{9}}{\mathrm{32}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}}= \\ $$$$=−\frac{\left({t}+\mathrm{1}\right)\left(\mathrm{9}{t}^{\mathrm{6}} −\mathrm{57}{t}^{\mathrm{4}} −\mathrm{104}{t}^{\mathrm{3}} +\mathrm{51}{t}^{\mathrm{2}} +\mathrm{24}{t}−\mathrm{11}\right)}{\mathrm{32}\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{9}\sqrt{\mathrm{2}}}{\mathrm{128}}\mathrm{ln}\:\frac{{t}+\mathrm{1}+\sqrt{\mathrm{2}}}{{t}+\mathrm{1}−\sqrt{\mathrm{2}}} \\ $$$$… \\ $$
